 设为首页
设为首页
 加入收藏
加入收藏
例1 如图所示,在盛水容器中,有4个体积完全相同的物体:A是一浮于水面的正方体木块;B是用线吊着浸没在水中的长方体铁块;C是悬浮在水中的空心钢球;D是圆台形石蜡块,它沉于容器底面并与容器底无缝隙紧密结合,试比较分析A、B、C、D所受浮力的情况.

分析
虽然A、B、C、D四个物体,它们的形状不同,组成的物体种类不同,有的是实心的、有的是空心的,浸入水中的深度也不同,但这些不同条件跟浮力的大小均无关,所以无需加以考虑.浮力的大小只跟液体的密度与排开液体的体积有关.因为它们是浸在同一种液体中,所以浮力的大小由 ![]() 而定,但D物体与容器底紧密结合,故浮力为零.由此可知,此题A、B、C、D四个物体所受浮力大小可以用下式来表示,即
而定,但D物体与容器底紧密结合,故浮力为零.由此可知,此题A、B、C、D四个物体所受浮力大小可以用下式来表示,即 ![]() 。
。
选题目的:通过本题加深学生对影响浮力大小的因素的理解.
例2 质量是5.4千克的铝球,若将它的一半浸入水中,铝球受到的浮力是多大?(
![]() )
)
分析 本题用阿基米德原理求解.需要知道液体的密度、物体排液体积.因为它浸入水中,水的密度已知,要弄清铝球排液体积,需要先用 ![]() 求出铝球的体积
求出铝球的体积
解 ![]() .
.
因为铝球一半浸入水中,
![]() .
.
运用阿基米德原理,
![]()
![]()
铝球受到的浮力是9.8牛.
选题目的:通过本题教会学生使用阿基米德原理公式解题的基本思路.
例3 有一木块,放入水中静止后,有 ![]() 的体积露在水面上,若将它放入另一种液体中时,有
的体积露在水面上,若将它放入另一种液体中时,有 ![]() 的体积浸入液体中,求液体的密度.
的体积浸入液体中,求液体的密度.
分析指导 设该木块的体积为 ![]() ,放入水中后有
,放入水中后有 ![]() 的体积露在水面,则意味着有
的体积露在水面,则意味着有 ![]() 的体积浸入水中,即
的体积浸入水中,即 ![]() .
.
受到的浮力 ![]() ,又因为放入另一种液体中漂浮时有
,又因为放入另一种液体中漂浮时有 ![]() 的体积浸在液体里,即
的体积浸在液体里,即 ![]() ,受到的浮力
,受到的浮力 ![]() .由于木块在水中和在液体中都是漂浮状态,其受到的浮力都等于重力.即
.由于木块在水中和在液体中都是漂浮状态,其受到的浮力都等于重力.即 ![]() .
.
则 ![]()
即 ![]()
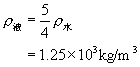
小结 此题是利用阿基米德原理解决密度问题的典型例题,而且条件较为隐蔽,在解决此类条件隐蔽的问题时,首先要认真分析题目中的一些关键词语,如上题中的“ ![]() 露出水面”,此处有两层含义:(1)物体是漂浮在液面,(2)
露出水面”,此处有两层含义:(1)物体是漂浮在液面,(2) ![]() .其次,要对物体的状态和受力做认真的分析,才能建立正确的方程.
.其次,要对物体的状态和受力做认真的分析,才能建立正确的方程.
选题目的:训练学生灵活应用阿基米德原理,并总结出一种计算液体密度的新方法.
例4 边长5厘米的正方体,浸没在水中,下表面距水面15厘米处,求出该物体受到的浮力.
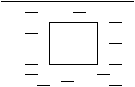
分析与解:此题可以用两种方法求解:方法一:根据浮力产生原因求浮力:F浮=F向上-F向下.
方法二:应用阿基米德原理求浮力:F浮=r水gV排,在求解过程中,一定要弄清各物理量的含义及单位.
方法一:由题意可知:下表面距水面深h2=15厘米,上表面距水面h1=10厘米,
解:F浮=F向上-F向下=P2žS-P1žS=r水žgh2žS-r水žgh1žS
=r水gS(h2-h1)=1.0×103千克/米3×9.8牛/千克×(5×10-2米)2×(5×10-2米)
=9.8×103千克/米3×1.25×10-4米3=1.225牛
方法二:根据阿基米德原理:
F浮=p水.gV排=1.0×103千克/米3×9.8牛/千克×(5×10-2)3米3
=1.225牛
答:该物体受到的浮力大小为1.225牛顿.
总结:在求解物理计算题时,一定要写清物理公式,带原始数据的国际单位,最后要写清答的内容.
选题目的:通过本题训练学生一题多解的能力,总结出求浮力的两种方法.
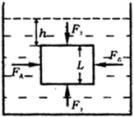
例5 如图,现有一正方体的物体悬浮于密度为 ![]() 的液体中,其边长为L,上表面距液面的深度为h,那么下表面距液面的深度即为
的液体中,其边长为L,上表面距液面的深度为h,那么下表面距液面的深度即为
![]() .请根据浮力产生的原因推导阿基米德原理.
.请根据浮力产生的原因推导阿基米德原理.
分析 由于对称关系,物块受到来自前后左右的压力应为平衡力,但上下表面所受的压力不同,
![]()
据
![]()
则
![]()
![]()
∴ ![]()
∴ ![]()
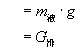
选题目的:让学生联系前一章的知识,从另一角度来加深理解阿基米德原理,为利用阿基米德原理解题奠定扎实得基础.