 设为首页
设为首页
 加入收藏
加入收藏
典型例题
一、图形中公式的灵活应用
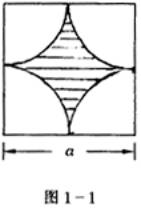
例1 用代数式表示图1—1中阴影部分面积S,并求当![]() 时阴影部分面积S(
时阴影部分面积S(![]() 取
取![]() )
)
分析 为了方便,可分别设正方形、扇形面积![]() 、
、![]() ,由图可知:
,由图可知:![]() ,进一步利用面积公式就可求出结果。
,进一步利用面积公式就可求出结果。
解:![]()

当![]() 时,
时,
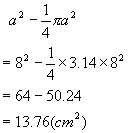
答:当![]() 时阴影部分面积为
时阴影部分面积为![]() 。
。
说明:计算此类阴影部分面积,常采取“叠加法”或“割补法”。要注意这种“聚零为整,化整为零”的思想方法在解题中的应用。
例2 已知梯形的上底是![]() ,下底是
,下底是![]() ,高是
,高是![]() ,面积是S。若
,面积是S。若![]() ,
,![]() 。求下底
。求下底![]() 。
。
解 根据加与减,乘与除互为逆运算
由![]() ,得
,得
![]() ,
,
![]() ,
,
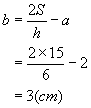
答:所求梯形的下底![]() 为
为![]() 。
。
说明:解此类题时,可先根据加与减,乘与除互为逆运算将公式变形,再由变形后的公式进行计算。
二、有关公式的应用题
某电影院有20排座位,已知第一排有18个座位,后面一排前一排多2个座位。写出计算第![]() 排的座位数
排的座位数![]() 的公式,并求第19排的座位数。
的公式,并求第19排的座位数。
分析 可将排数与对应的座位数列表如下:
|
排数 |
每排座位数 |
|
1 2 3 4 5 … |
18 20 22 24 26 … |
第一排为![]() 个座位;第二排有
个座位;第二排有![]() 个座位;第三排有
个座位;第三排有![]() 个座位……,由此可知座位数
个座位……,由此可知座位数![]() 与排数
与排数![]() 之间的关系。
之间的关系。
解 座位数![]() 与排数
与排数![]() 之间关系为:
之间关系为:
![]()
当![]() 时,
时,
![]()
点评 此题需从反映数量关系的一些数据中分析出公式,进而求代数式的值,其中包含“由特殊到一般,又由一般到特殊”的思维方法,解题时要注意体会。
三、教材例题分析
例1体现了这一小节的基本要求,就是直接利用公式求解实际问题。
例2是一个求环形面积的题,这里除了应用圆面积公式之外,还渗透了一点公式导出的思想方法。接下来,课文借助一个表格,给出了一个实际问题中两个量之间的关系,借助于这个表格,利用代数式,就可以推导出反映这两个量之间关系的公式了。
例3通过一个具体实例展示了通过观察、归纳得到公式,应用公式的整个过程,充分体现了由特殊到一般,再由一般到特殊的认知规律,是一个培养学生分析问题、解决问题能力的好素材。