第六节 平面向量的数量积及运算律

典型例题

　　例1．已知 、 、 是三个非零向量，则下列命题中真命题的个数为（    ）

　　① ；　　② 、 反向

　　③ ；　　④

　　A．1   B．2   C．3  D．4

　　分析：需对以上四个命题逐一判断，依据有两条，一是向量数量积的定义；二是向量加法与减法的平行四边形法则．①中∵ ，∴由 及 、 为非零向量可得 ，∴ 或 ，∴ 且以上各步均可逆，故命题①是真命题．②中若 、 反向，则 、 的夹角为 ，∴ 且以上各步均可逆，故命题②是真命题．③中当 时，将向量 、 的起点确定在同一点，则以向量 、 为邻边作平行四边形，则该平行四边形必为矩形，于是它的两对角线长相等，即有 ．反过来，若 ，则以 、 为邻边的四边形为矩形，所以有 ，因此命题③是真命题．④中当 但 与 的夹角和 与 的夹角不等时，就有 ，反过来由 也推不出 ．故命题④是假命题．

　　［答案］C

　　小结：（1）两向量同向时，夹角为0（或 ）；而反向时，夹角为 （或 ）；两向量垂直时，夹角为 ．因此当两向量共线时，夹角为0或 ，反过来若两向量的夹角为0或 ，则两向量共线．

　　（2）对于命题④我们可以改进为： 既不是 的充分条件也不是必要条件．

　　例2．已知 ， ，当（l） （2） ，（3） 与 的夹角为 时，分别求 与 的数量积。

　　分析：已知 与 ，求 ，只需确定其夹角 ，须注意到 时，有 和 两种可能。

　　解：（1） ，若 与 同向，则 ，

　　∴ ；

　　若 与 反向，则 ，

　　∴ ，

　　（2）当 时， ，

　　∴ ，

　　（3）当 与 的夹角为 时，

　　 .

　　小结：（1）对于数量积 ，其中 的取值范围是 ；

　　（2）非零向量 和 ， ；（3）非零向量 和 共线的充要条件是   ．

　　例3．设 ，则 与 的夹角 的余弦值为＿＿＿＿＿．

　　分析：要求夹角需先求出 的值。

　　解： ， ．把 代入得 ．由 ，得 于是 ．

　　小结：本题涉及了平面向量的数量积的概念，性质 以及有关运算律，体现了较强的综合性．

　　例4．已知 ，当 时，求实数 的值．

　　分析：求一个实数的值，运用方程的思想，建立一个方程，通过解方程使问题得解．

　　解： ， ． ， ，即 ， ※．把 ， 代入※式，得

　　例5．用向量方法证明：正方形的对角线互相垂直．

　　分析：运用数量积为零来证明．

　　证明：设正方形为 ，对角线为 和 ，以下只需证明 ．

　　 ， ，

　　 ．

　　 正方形 中，

　　，

　　 ，即对角线互相垂直．

　　小结：本题意在让学生了解用数量积证明平面几何中的垂直问题，

　　例6．已知非零向量 和 夹角为 ，且 ，求证： ．

　　分析：欲证两个向量垂直只需证明它们的数量积为零．

　　证明：因为 和 夹角为 ，所以 ；又因为 ，所以 ，即 ， ， 即 ．因为 ，把 代入上式消去 得 ．所以 ．

　　小结：这也是垂直的证明问题，但不是从平面几何的角度，而是直接从数量积的角度给出条件，再运用数量积的有关知识解决问题．

　　例7． 如图，已知 中， 是直角， ， 是 的中点， 是 上的一点，且 . 求证： .

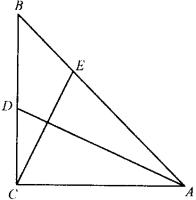
　　分析：借助向量垂直的充要条件解题，即证明 .

　　证明：设此等腰直角三角形的直角边长为 ，则

　　

　　　　　

　　　　　

　　　　　 .

　　所以  .

　　小结：用向量方法证明几何问题时，一般应把已知和结论转化成向量的形式，再通过相应的向量运算完成证明，不难发现，利用实数与向量的积可证明共线、平行、长度关系等方面的几何问题，利用向量的数量积可解决长度关系、角度、垂直等几何问题。