 设为首页
设为首页
 加入收藏
加入收藏
例1 三条直线两两相交,由这三条直线所确定平面的个数是( )
A.1 B.2 C.3 D.1或3
分析 本题显然是要应用推论2判断所能确定平面的个数,需要在空间想象出这三条直线所有不同位置的图形,有如下图的三种情况(如图):

答案:D.
说明 本题启发我们考虑问题不要只局限于平面图形,应养成在三维空间考虑问题的习惯.
例2 一条直线与三条平行直线都相交,求证这四条直线共面.
分析 先将已知和求证改写成符号语言.证明诸线共面,可先由其中的两条直线确定一个平面,然后证明其余的直线均在此平面内.也可先由其中两条确定一个平面 ![]() ,另两条确定平面
,另两条确定平面 ![]() ,再证平面
,再证平面 ![]() ,
, ![]() 重合.
重合.
已知: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
求证:直线 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共面.
共面.
证明 ∵
![]() ,
,
∴ ![]() ,
, ![]() 确定一个平面
确定一个平面 ![]() .
.
∵ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,故
,故 ![]() .
.
又 ∵
![]() ,
∴
,
∴
![]() ,
, ![]() 确定一个平面
确定一个平面 ![]() .
.
同理可证 ![]() .
.
∴ ![]() ,且
,且 ![]() .
.
∵ 过两条相交直线
![]() ,
, ![]() 有且只有一个平面,故
有且只有一个平面,故 ![]() 与
与 ![]() 重合
重合
即直线 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共面.
共面.
说明 本例是新教材第9页第9题的一个简单推广,还可推广到更一般的情形.本例证明既采用了归一法,同时又采用了同一法.这两种方法是证明线共面问题的常用方法.在证明 ![]() 时,也可以用如下反证法证明:
时,也可以用如下反证法证明:
假设直线 ![]() ,则
,则 ![]() 一定与
一定与 ![]() 相交,此时直线
相交,此时直线 ![]() 与
与 ![]() 内的所有直线都不会平行,这显然与
内的所有直线都不会平行,这显然与 ![]() 矛盾.故
矛盾.故 ![]() .
.
例3 已知 ![]() 在平面
在平面 ![]() 外,它的三边所在的直线分别交平面
外,它的三边所在的直线分别交平面 ![]() 于
于 ![]() ,
, ![]() ,
, ![]() 三点,证明
三点,证明 ![]() ,
, ![]() ,
, ![]() 三点在同一条直线上.
三点在同一条直线上.
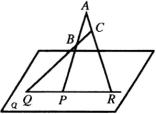 分析 如图所示,欲证
分析 如图所示,欲证 ![]() ,
, ![]() ,
, ![]() 三点共线,只须证
三点共线,只须证 ![]() ,
, ![]() ,
, ![]() 在平面
在平面 ![]() 和平面
和平面 ![]() 的交线上,由
的交线上,由 ![]() ,
, ![]() ,
, ![]() 都是两平面的公共点而得证.
都是两平面的公共点而得证.
证明:
∵ ![]() ,
, ![]() ,
,
∴ ![]() 是平面
是平面 ![]() 与平面
与平面 ![]() 的交线.
的交线.
又 ∵
![]() ,
,
∴ ![]() 且
且 ![]() 平面
平面 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
说明 证明点共线的一般方法是证明这些点是某两个平面的公共点,由公理2,这些点都在这两平面的交线上.
例4 如图所示, ![]() 与
与 ![]() 不在同一个平面内,如果三直线
不在同一个平面内,如果三直线 ![]() 、
、 ![]() 、
、 ![]() 两两相交,证明:三直线
两两相交,证明:三直线 ![]() 、
、 ![]() 、
、 ![]() 交于一点.
交于一点.
分析 证明三线共点的一般思路是:先证明两条直线交于一点,再证明该点在第三条直线上即可.
证明 由推论2,可设 ![]() 与
与 ![]() ,
, ![]() 与
与 ![]() ,
, ![]() 与
与 ![]() 分别确定平面
分别确定平面 ![]() ,
, ![]() ,
, ![]() .
.
取 ![]() ,则
,则 ![]() ,
, ![]() .
.
又因 ![]() ,则
,则 ![]() (公理2),
(公理2),
于是 ![]() ,
,
故三直线 ![]() 、
、 ![]() 、
、 ![]() 共点.
共点.
说明 空间中证三线共点有如下两种方法:
(1)先确定两直线交于一点,再证该点是这两条直线所在两个平面的公共点,第三条直线是这两个平面的交线,由公理2,该点在它们的交线上,从而得三线共点.
(2)先将其中一条直线看做是某两个平面的交线,证明该交线与另两直线分别交于两点,再证这两点重合.从而得三线共点.