 设为首页
设为首页
 加入收藏
加入收藏
例1 甲、乙两个人独立地破译一个密码,他们能译出密码的概率分别为![]() 和
和![]() ,求:
,求:
(1)两个人都译出密码的概率;
(2)两个人都译不出密码的概率;
(3)恰有1个人译出密码的概率;
(4)至多1个人译出密码的概率;
(5)至少1个人译出密码的概率.
分析:我们把“甲独立地译出密码”记为事件![]() ,把“乙独立地译出密码”记为事件
,把“乙独立地译出密码”记为事件![]() ,显然
,显然![]() 为相互独立事件,问题(1)两个都译出密码相当于事件
为相互独立事件,问题(1)两个都译出密码相当于事件![]() 、
、![]() 同时发生,即事件
同时发生,即事件![]() .问题(2)两人都译不出密码相当于事件
.问题(2)两人都译不出密码相当于事件![]() .问题(3)恰有1个人译出密码可以分成两类:
.问题(3)恰有1个人译出密码可以分成两类:![]() 发生
发生![]() 不发生,
不发生,![]() 不发生
不发生![]() 发生,即恰有1个人译出密码相当于事件
发生,即恰有1个人译出密码相当于事件![]() .问题(4)至多1个人译出密码的对立事件是两个人都未译出密码,即事件
.问题(4)至多1个人译出密码的对立事件是两个人都未译出密码,即事件![]() .由于
.由于![]() 、
、![]() 是独立事件,上述问题中,
是独立事件,上述问题中,![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() 是相互独立事件,可以用公式计算相关概率.
是相互独立事件,可以用公式计算相关概率.
解:记“甲独立地译出密码”为事件![]() ,“乙独立地译出密码”为事件
,“乙独立地译出密码”为事件![]() ,
,![]() 、
、![]() 为相互独立事件,且
为相互独立事件,且![]() .
.
(1)两个人都译出密码的概率为:
![]() .
.
(2)两个人都译不出密码的概率为:
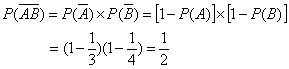
(3)恰有1个人译出密码可以分为两类:甲译出乙未译出以及甲未译出乙译出,且两个事件为互斥事件,所以恰有1个人译出密码的概率为:
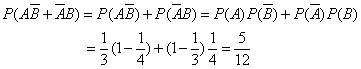
(4)“至多1个人译出密码”的对立事件为“有两个人译出密码”,所以至多1个人译出密码的概率为:
![]() .
.
(5)“至少有1个人译出密码”的对立事件为“两人未译出密码”,所以至少有1个人译出密码的概率为:
![]() .
.
说明:如果需要提高能译出密码的可能性,就需要增加可能译出密码的人,现在可以提出这样的问题:若要达到译出密码的概率为99%,至少需要像乙这样的人多少个?我们可以假设有![]() 个像乙这样的人分别独立地破译密码,此问题相当于
个像乙这样的人分别独立地破译密码,此问题相当于![]() 次独立重复试验,要译出密码相当于至少有1个译出密码,其对立事件为所有人都未译出密码,能译出密码的概率为
次独立重复试验,要译出密码相当于至少有1个译出密码,其对立事件为所有人都未译出密码,能译出密码的概率为![]() ,按要求,
,按要求,![]() ,故
,故![]() ,可以计算出
,可以计算出![]() ,即至少有像乙这样的人16名,才能使译出密码的概率达到99%.
,即至少有像乙这样的人16名,才能使译出密码的概率达到99%.
 例2
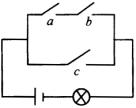
如图,开关电路中,某段时间内,开关
例2
如图,开关电路中,某段时间内,开关![]() 开或关的概率均为
开或关的概率均为![]() ,且是相互独立的,求这段时间内灯亮的概率.
,且是相互独立的,求这段时间内灯亮的概率.
分析:我们把“开关![]() 合上”记为事件
合上”记为事件![]() ,“开关
,“开关![]() 合上”记为事件
合上”记为事件![]() ,“开关
,“开关![]() 合上”记为事件C,
合上”记为事件C,![]() 是相互独立事件且由已知,它们的概率都是
是相互独立事件且由已知,它们的概率都是![]() ,由物理学知识,要求灯亮,有两种可能性,一个是
,由物理学知识,要求灯亮,有两种可能性,一个是![]() 、
、![]() 两开关合上,即事件
两开关合上,即事件![]()
![]() 发生,另一个是
发生,另一个是![]() 开关合上,即事件
开关合上,即事件![]() 发生,也就是灯亮相当于事件
发生,也就是灯亮相当于事件![]() 发生.
发生.
解:分别记“开关![]() 合上”、“开关
合上”、“开关![]() 合上”、“开关
合上”、“开关![]() 合上”为事件
合上”为事件![]() ,由已知,
,由已知,![]() 是相互独立事件且概率都是
是相互独立事件且概率都是![]() .
.
开关![]() 、
、![]() 合上或开关
合上或开关![]() 合上时灯亮,所以这段时间内灯亮的概率为:
合上时灯亮,所以这段时间内灯亮的概率为:
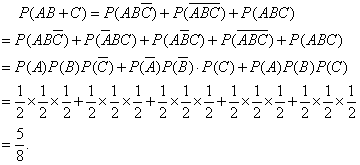
说明:本题的解题过程中,灵活使用了概率中的一些符号,比如,![]() 表示事件
表示事件![]() 与事件
与事件![]() 同时发生,
同时发生,![]() 表示事件
表示事件![]() 与事件
与事件![]() 至少有一个发生,
至少有一个发生,![]() 表示
表示![]() 与
与![]() 至少有一个发生,所以分成了三个互斥事件:
至少有一个发生,所以分成了三个互斥事件:![]() 发生
发生![]() 不发生,
不发生,![]() 不发生
不发生![]() 发生,
发生,![]() 与
与![]() 都发生,而其中
都发生,而其中![]() 不发生
不发生![]() 发生即
发生即![]() ,又
,又![]() 不发生即
不发生即![]() 与
与![]() 至少有一个不发生,从而
至少有一个不发生,从而![]() 又分成了三个互斥事件:
又分成了三个互斥事件:![]() 、
、![]() 、
、![]() ,符号语言的正确理解与使用,不仅是提高数学能力的需要,而且也使数学解题过程简便明了,一些数学结论表述更加方便.我们可以尝试理解并领会下列结论:
,符号语言的正确理解与使用,不仅是提高数学能力的需要,而且也使数学解题过程简便明了,一些数学结论表述更加方便.我们可以尝试理解并领会下列结论:
![]() ,
,
![]()
![]() ,
,![]()
![]() .
.
例3 掷三颗骰子,试求:
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率.
分析:我们把三颗骰子出现1点或6点分别记为事件![]() ,由已知,
,由已知,![]() 是相互独立事件.问题(1)没有1颗骰子出现1点或6点相当于
是相互独立事件.问题(1)没有1颗骰子出现1点或6点相当于![]() ,问题(2)恰有一颗骰子出现1点或6点可分为三类:
,问题(2)恰有一颗骰子出现1点或6点可分为三类:![]() ,三个事件为互斥事件.问题(1)可以用相互独立事件的概率公式求解,问题(2)可以用互斥事件的概率公式求解.
,三个事件为互斥事件.问题(1)可以用相互独立事件的概率公式求解,问题(2)可以用互斥事件的概率公式求解.
解:记“第1颗骰子出现1点或6点”为事件![]() ,由已知
,由已知![]() 是相互独立事件,且
是相互独立事件,且![]() .
.
(1)没有1颗骰子出现1点或6点,也就是事件![]() 全不发生,即事件
全不发生,即事件![]() ,所以所求概率为:
,所以所求概率为:
![]() .
.
(2)恰好有1颗骰子出现1点或6点,即![]() 发生
发生![]() 不发生
不发生![]() 不发生或
不发生或![]() 不发生
不发生![]() 发生
发生![]() 不发生或
不发生或![]() 不发生
不发生![]() 不发生
不发生![]() 发生,用符号表示为事件
发生,用符号表示为事件![]() ,所求概率为:
,所求概率为:
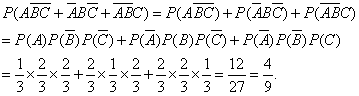
说明:再加上问题:至少有1颗骰子出现1点或6点的概率是多少?我们逆向思考,其对立事件为“没有一颗骰子出现1点或6点,即问题(1)中的事件,所求概率为![]() ,在日常生活中,经常遇到几个独立事件,要求出至少有一个发生的概率,比如例1中的至少有1个人译出密码的概率,再比如:有两门高射炮,每一门炮击中飞机的概率都是0.6,求同时发射一发炮弹,击中飞机的概率是多少?把两门炮弹击中飞机分别记为事件A与B,击中飞机即
A与B至少有1个发生,所求概率为
,在日常生活中,经常遇到几个独立事件,要求出至少有一个发生的概率,比如例1中的至少有1个人译出密码的概率,再比如:有两门高射炮,每一门炮击中飞机的概率都是0.6,求同时发射一发炮弹,击中飞机的概率是多少?把两门炮弹击中飞机分别记为事件A与B,击中飞机即
A与B至少有1个发生,所求概率为![]()
![]()
![]()
![]() .
.
例4 某工厂的产品要同时经过两名检验员检验合格方能出厂,但在检验时也可能出现差错,将合格产品不能通过检验或将不合格产品通过检验,对于两名检验员,合格品不能通过检验的概率分别为![]() ,不合格产品通过检验的概率分别为
,不合格产品通过检验的概率分别为![]() ,两名检验员的工作独立.求:(1)一件合格品不能出厂的概率,(2)一件不合格产品能出厂的概率.
,两名检验员的工作独立.求:(1)一件合格品不能出厂的概率,(2)一件不合格产品能出厂的概率.
分析:记“一件合格品通过两名检验员检验”分别记为事件![]() 和事件
和事件![]() ,问题(1)一件合格品不能出厂相当于一件合格品至少不能通过一个检验员检验,逆向考虑,其对立事件为合格品通过两名检验,即
,问题(1)一件合格品不能出厂相当于一件合格品至少不能通过一个检验员检验,逆向考虑,其对立事件为合格品通过两名检验,即![]() 发生,而
发生,而![]() 的概率可以用相互独立事件的概率公式求解.我们把“一件不合格品通过两名检验员检验”分别记为事件
的概率可以用相互独立事件的概率公式求解.我们把“一件不合格品通过两名检验员检验”分别记为事件![]() 和事件
和事件![]() ,则问题(2)一件不合格品能出厂相当于一件不合格品同时通过两名检验员检验,即事件
,则问题(2)一件不合格品能出厂相当于一件不合格品同时通过两名检验员检验,即事件![]() 发生,其概率可用相互独立事件概率公式求解.
发生,其概率可用相互独立事件概率公式求解.
解:(1)记“一件合格品通过第i名检验员检验”为事件![]() ,“一件合格品不能通过检验出厂”的对立事件为“一件合格品同时通过两名检验员检验”,即事件
,“一件合格品不能通过检验出厂”的对立事件为“一件合格品同时通过两名检验员检验”,即事件![]() 发生.
发生.
所以所求概率为![]()
![]() .
.
(2)“一件不合格品能通过第i名检验员检验”记为事件![]() ,“一件不合格品能出厂”即不合格品通过两名检验员检验,事件
,“一件不合格品能出厂”即不合格品通过两名检验员检验,事件![]() 发生,所求概率为:
发生,所求概率为:
![]() .
.
例5 某大学的校乒乓球队与数学系乒乓球队举行对抗赛,校队的实力比系队强,当一个校队队员与系队队员比赛时,校队队员获胜的概率为0.6.现在校、系双方商量对抗赛的方式,提出了三种方案:(1)双方各出3人;(2)双方各出5人;(3)双方各出7人.三种方案中场次比赛中得胜人数多的一方为胜利.问:对系队来说,哪一种方案最有利?三种方案中,哪一种方案系队获胜的概率更大一些,哪一种方案对系队更有利.进行几场比赛相当于进行几次独立重复试验,可以用n次独立重复试验中某事件发生![]() 次的概率方式解题.
次的概率方式解题.
解:记一场比赛系队获胜为事件![]() ,事件
,事件![]() 的对立事件为校队获胜,所以
的对立事件为校队获胜,所以![]()
用方案(1),![]() 发生两次为系队胜,
发生两次为系队胜,![]() 发生3次也为系队胜,所以系队胜的概率为:
发生3次也为系队胜,所以系队胜的概率为:
![]()
用方案(2),![]() 发生3、4、5次为系队胜.
发生3、4、5次为系队胜.
所以系队胜的概率为:
![]()
![]()
![]()
用方案(3),![]() 发生4、5、6、7次为系队胜.
发生4、5、6、7次为系队胜.
所以系队胜的概率为:
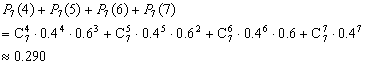
比较可以看出,双方各出3个人对系队更有利,获胜概率为0.352.
实际上,对弱队而言,比赛场数越少,对弱队越有利,侥幸取胜的可能性越大.
说明:在日常生活中,经常出现方案的比较问题,或者方案是否合理的论证问题,比如产品抽查,抽检几件比较合理,因为抽多了浪费人力,抽少了容易让不合格产品出厂.设备维修安排几位维修工较合理,安排人员过多造成浪费,安排人员过少设备不能及时维修,这些问题都可以用本题的思维方法,先设计一个独立重复试验,然后抓某个事件发生的概率,看概率是否较小.
我们可以看例子:10台同样的设备,各自独立工作,设备发生故障的概率为0.01,现在安排1名维修工,试说明这种配备是否合理?10台设备各自独立工作,相当于10次独立重复试验,有1名维修工人,若两台以上机器发生故障则得不到及时维修,其对立事件为至多1台机器发生故障,我们可以得到多于1台机器发生故障的概率为:
![]() .
.
从结果来看,得不到及时维修的概率很小,安排一人维修比较合理.