第七节 相互独立事件同时发生的概率

概率分布——二项分布

　　独立重复试验，又叫做贝努里试验，是在同样的条件下重复地、各次之间相互独立地进行的一种试验．在这种试验中，每一次试验的结果只有两种，即某事件要么发生，要么不发生，并且任何一次试验中发生的概率都是一样的．在 次独立重复试验中某事件恰好发生 次的概率（ 且 ）组成“离散”型随机变量的一种相当重要的概率分布——二项分布．

　　关于在n次独立重复试验中某事件恰好发生k次的概率计算公式，在此给出一般性的推导：已知 是某随机试验中可能出现的事件，且 ，现在把这个试验独立地重复进行 次，要求事件 恰好发生 次的概率．

　　首先，在 次试验的总结果中，有些试验结果是 ，有些试验结果是 ，所以总结果是几个 与几个 的一种搭配．要求总结果中事件 恰好发生 次，就是 个 与 个 的一种搭配．而合乎这个要求的搭配，又因 与 出现的先后次序不同而可能有许多种．在 次试验的总结果中，含 个 以及 个 的搭配的种数，相当于从 个号码中任取 个号码的不同取法的种数 种，而所有这些引起的搭配显然都是等可能的，并且均是互斥的．”

　　其次，根据相互独立事件的概率的乘法公式，合乎上述要求的每一种搭配发生的概率都是

　　其实 是二项式 展开式中的第 项，因此也把这个公式叫做二项分布公式．

（选自《概率论》）

把握机会，成自险出

　　掷骰子是一种机会游戏，骰子是在立方体（一般是牛骨制成）的六个面上分别刻上1个，2个，3个，4个，5个，6个“点儿”，两人赌博时，掷出的骰子向上的面上点多者赢，这纯属碰运气，事实上，每次掷扔，每个面朝上的机会均等，都是 ．骰子这个玩艺儿历史悠久，考古学家从伊拉克北部发现了公元前2000多年前的骰子，虽然自古各国都明令禁赌，但大多数国家屡禁不止．赌博有百害但也有一功，就是它引起了一些数学家的注意，并从中酝酿提炼出一门称为概率论的数学分支，例如伽利略、帕斯卡、赛马都是最早研究赌博中的概率问题的代表人物．

　　概率已经成了世界公认的数学专用名词，其实称它为“机会”更直白更准确，也许是由于嫌机会这个词“太土”，才用了“概率”这两个似显文雅的专业名词．事实上，叫什么也无所谓，你看玫瑰花，不管把它称为什么，看起来还是那么美，闻起来还是那么香．我们知道了，所谓概率大就是机会大，例如电视台天气预报说本市明天降水的概率是40％，就是在告诉我们明天下雨（雪）的机会是40％．如此说来，掷骰子掷出偶点儿的概率是 ，掷硬币掷出国徽面的概率是 ，生小孩生男孩的概率也是 等等；当然并不是什么事情出现的机会都是一半对一半，一般需要进行认真的计算．下面是几个小实例．

　　（1）m个红球，n个白球，其质地和大小都一样，放入一个布袋中，搅拌后从中任意摸出r个球， ，问这r个球全是红球的概率是多少．

　　从 个球中任意抽取r个球的方式数为 ，从 m个红球中抽出 r个的可能方式有 种，所以从袋子中摸出的r个球全红的机会的大小为

　　　　

　　　　　　　　

　　例如袋子里原有10个红球，10个白球，抽得10个球全红的机会为

　　只有大约百万分之五的可能抽得的十个球全红（或全白），这个机会太小，几乎是不能实现的事．

　　（2）甲乙二人赌博，各下赌注500元，约定先胜三局者把1000元赌注全拿走；设两人赌技相当，赌了三局，甲以2：1暂时领先，这时忽闻人呼：抓赌的来了！甲乙落荒而逃，到一个隐蔽处去分赌本，问这时应如何分这1000元赌本才使两赌徒都心服口服？

　　一种方案是没有赌完，各拿回自己的500元赌本，但甲不同意，他认为自己已经多赢一局，应多拿．第二种方案是全归甲；乙不服，乙说再赌下去也许他会连扳两局呢！第三种方案是按赢的比例分配，甲拿1000元 的，乙拿 。仔细分析起来，按比例似合乎人们的心理习惯，但也并不合理．事实上，甲乙若继续赌下去，至多再两局可见胜负，即平时所言的“五打三胜”，两局有四种可能性：甲连胜，甲乙各胜一局甲先胜，乙甲各胜一局乙先胜，乙连胜．由于2人赌技相同，以上四种可能出现的机会是一致的，而前三种结果都造成甲最后的胜利，所以甲在此未进行到底的赌博中得胜的机会是 ，申应分得赌注750元．

　　历史上，17世纪赌徒梅累（Mere）向帕斯卡提出这个问题（本题数据有改动），帕氏苦想很久才得到解答，1654年7月29日，帕斯卡把他的解法寄给了费马，两人继续通信深入讨论了与此有关的概率问题．16世纪意大利数学家卡当写了《论赌博》一书，算是概率方面的第一本著作，1713年，雅各·贝努利出版名著《猜度术》，1760年法国的蒲丰写出《偶然性的算术试验》，1812年拉普拉斯出版《分析概率论》，1896年，我国翻译成汉语的第一本概率著作是《决疑数学》；我国已是当今概率方面的强国，北大已故教授许宝騄等人对现代概率论与数理统计有世界领先水平的工作．

　　（3）n个人 随机地排成一路纵队。紧跟在 后面的概率是多少？

　　n个人的随机排列共n！种可能， 紧跟 的事件有n－种可能，即 为排头， 排第二，或 排第二， 排第三，…， 排第n－1， 排队尾．其他的n－2人有 种排法，所以所求概率为

　　（4）从有10条金鱼的鱼缸中提出一条金鱼后再放回鱼缸，这样一直抓过5次鱼，指定的一条鱼被抓3次的概率是多少？

　　因为第一次抓有10种可能性，第二次，…，第五次也都有10种可能，共计 种可能性；在5次抓鱼中指定的鱼抓住3次的各种可能为 种，每种可能出现时其余2次捉鱼的方式有 ，故所求概率为：

　　让我们从数学上把上面几个实例略加总结，在现实世界当中，许多现象是事先无法断定其结果的，例如掷骰子，骰子没有落稳之前，谁也不知道它朝上的一面是几个点儿，每掷一次，就是一次随机试验，每次随机试验可能得到的结果称为基本事件．例如掷骰子这种随机试验共有六个可能的结果，它的基本事件个数是 ．这些基本事件出现的可能性或称机会是均等的，其中我们关心的事件A若可能出现m次，例如掷骰子出现六个点是我们关心的事件A，则称 为事件A的古典概率，P（A）中的P是Probability的字头，掷骰子中事件A的概率 ．在古典概率当中基本事件是有限的．冠以“古典”两个字是因为在概率的初创时期，研究赌博等活动时的思路与方法就是如此，它主要借助于组合数学的一些初等的古典的计数方法来进行计算。

　　（5）已知事件A的概率是p，条件不变的情况下试验n次，事件A出现r次的概率是多少？

　　例如掷骰子，出现6个点的概率为 ，若共掷了6次，掷出3次六个点儿的“好事儿”的概率是多少？或者一台机床加工零件的合格率是 ，如果这台机床共产生了8个零件，其中有7个是合格品的概率是多少？

　　这种问题涉及的是每次随机试验只有成功或失败两种结果，所以格外引人注意；同时每次试验是独立进行的，例如掷骰子，上次掷出几个点，并不影响下一次的成败（6个点算成功），每次试验的条件是相同的，从而每次试验成败的机会是一致的．

　　这种问题可以直观地转述成如下问题：

　　在n个袋子里都放入M个红球和 个白球，袋子编号为1，2，…，n，依次从每个袋子中各取出一个球为n次试验，那么从一个袋子中抽得的是红球这种事件A的概率为 ，问的是抽出的这n个球和恰有r个是红球的概率是多少？这里把每两个球都视为相异的．

　　从n个袋子里各取一球的可能性为 种，下面计算其中恰有r个球是红色的可能性有几种．r个红球分别来自r个袋子，这些红球出自那些袋子的可能性有 种；对这每种可能性，从其每袋中抽一红球的可能性有 种，从其余的 个袋子中各抽一个白球，其可能性是 种，所以抽出的n个球中恰有r个红球这一事件A的可能性有 种，从而P（A）为

　　　 , 　　　（1）

　　如果把从一个袋子里抽得一只红球算做一次胜利，抽得白球算做一次失败，则每次失败的概率为 ，令 ，每次成功的概率为p，（1）可改写成

　　　　　 ，　　　　　　　　　　　 （2）

　　真是巧得很，P（A）恰为 展开式的第 项，所以（2）表达的概率也称为“二项概率”．

　　回到开始的两个具体问题．6次掷骰子出了三次“六个点儿”， ，代入二项概率公式（2）得

　　生产8个零件7个合格的那个问题中， ，代入公式（2）得

　　即连产8个零件有7个合格的概率是0.336，这种可能性并不大！可见合格率低于80％是不能令人满意的．

　　《汉书·高帝纪》上记载了刘邦的话曰：“夫运筹帷幄之中，决胜千里之外，吾不如子房．”子房者，即张子房，又名张良．刘邦出身草莽，个人成分流氓，他起兵夺天下，靠的是张良等人出谋划策，确定取胜的战略战术．当然常胜将军并不是仗仗皆胜，只要胜多做少，每次参战取胜的概率大于八成就算是常胜将军了．在现实社会当中，人们在拼搏，在抗争，办事之前必须要对成功与失败的机会之大小有一个估算，不能指望什么事都是“零风险”的，一般而言失败的概率总会大于零，只求其足够小就是了，概率方法提供了我们估算成败可能性大小的数学方法，是一种十分中用十分有趣够数学分支．

　　常言道，抓住机遇，成自险出，工于计算，胸有成竹．

赌棍“考验”数学家

　　对概率的兴趣，是由保险事业的发展而产生的，但刺激数学家思考概率论问题的却来自赌博者的请求．

　　传说，17世纪中叶，法国贵族公子梅累参加赌博，和赌友掷骰子，各押赌注32个金币．双方约定，梅累如果先掷出三次6点，或者赌友先掷出三次4点，就算赢了对方．赌博进行了一段时间，梅累已经两次掷出6点，赌友已经一次掷出4点．这时候梅累接到通知，要他马上陪国王接见外宾，赌博只好中断了．这就碰到一个问题：两个人应该怎样分这64个金币才算合理呢？

　　赌友说，他要再碰上两次4点，或梅累要再碰上一次6点就算赢，所以梅累分64个金币的 ，自己分64个金币的 ．梅累急辩说，不时，即使下一次赌友掷出了4点，他还可以得 ，即32个金币；再加上下一次还有一半希望得16个金币，所以他应该分64的个金币的 ，赌友只能分得64个金币的 ．两人到底谁说得对呢？

　　梅累为这问题苦恼好久，最后他不得不向法国数学家、物理学家帕斯卡请教，请求他帮助作出公正的裁判，这就成为有趣的“分赌注”问题．

　　帕斯卡是17世纪有名的“神童”数学家．可是，梅累提出的“分赌注”的问题，却把他难住了．他苦苦思考了近三年，到1654年才算有了点眉目，于是写信给他的好友费马，两人讨论结果，并取得了一致的意见：梅累的分法是对的，他应得64个金币的 ，赌友应得64个金币的 ．这时有位荷兰的数学家惠更斯，在巴黎听到这件新闻，也参加了他们的讨论．惠更斯把讨论的结果写成一本书叫做《论赌博中的计算》（1657年），这就是概率论的最早一部著作．

　　除保险事业之外，各行各业都经常会碰到“某事件发生的可能性大小”的问题．因此，概率论问世后，在各方面得到了广泛的应用．可是，到了19世纪末，法国数学家贝特朗奇发现了一个非常有趣的怪论．他研究了下面一个问题：

　　“设圆内接等边三角形的边长为 ，在圆上任作一弦，问其长度超过 的概率是多少？”

　　贝特朗奇算出了三种不同的答案，三种解法似乎又都有道理。人们把这种怪论称为概率怪论，或贝特朗奇怪论．

　　贝特朗奇的解法如下：

　　解法一：任取一弦 ，过点 作圆的内接等过三角形（如图1）．因为三角形内角 所对的孤，占整个圆周的 ．显然，只有点 落在这段弧上时， 弦的长度才能超过正三角形的过长 ，故所求概率是 .

　　解法二：任取一弦 ，作垂直于 的直径 ．过点 作等过三角形，交直径于 ，并取 的中点 （如图2）．容易证明 ．我们知道，弦长与弦心距有关．一切与 垂直的弦，如果通过 线段的，其弦心距均小于 ，则该弦长度就大于等边三角形边长，故所求概率是 .

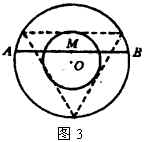
　　解法三：任取一弦 ．作圆内接等边三角形的内切圆（如图3），这个圆是大圆的同心圆，而且它的半径是大圆的 ，它的面积是大圆的 ，设 是弦 的中点，显然，只有中点落在小圆内时， 弦才能大于正三角形的边长．因此所求的概率是 .

　　细细推敲一下，三种解法的前提条件各不相同：

　　第一种假设了弦的端点在四周上均匀分布；第二种假设弦的中点在直径上均匀分布；第三种假设弦的中点在小圆内均匀分布．由于前提条件不同，就导致三种不同的答案．这是因为在那时候概率论的一些基本概念（如事件、概率及可能性等）还没有明确的定义，作为一个数学分支来说，它还缺乏严格的理论基础，这样，对同一问题可以有不同的看法，以致产生一些奇谈怪论．

　　概率怪论的出现，迫使数学家们注意概率基础理论的研究．1933年，苏联数学家柯尔莫哥洛夫提出了概率论公理化结构，明确了概率的各种基本概念，使概率论成为严谨的数学分支．