 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
学习直线、射线与线段的一般数学方法和技巧
一、把握几何概念与图形的内在联系
形的概念起源于现实世界.人类生活在丰富多采,千变万化的大千世界中,在我们的周围存在着大小不一、形状各异的各种物体,小至纸、笔、针、线,大至日、月、星辰,它们都具有一定的形状、大小,并在空间占有一定的位置.如果我们不管它们的其它性质,而只注意它们的形状、大小、位置,就抽象出几何图形,分析这些图形的特征,形成相应的概念,并用文字、符号把概念表述出来.在几何的入门阶段,以图形作基本依托,把握几何概念所反映的几何图形的本质属性,成为最基本的数学方法,这样,在运用数学概念进行思维或者在口头上,书面上表述的时候,头脑中就可以呈现出相应的图形,以及这个图形的本质特征,而不是形式上地记住定义的字句.
例1 判断下列说法是否正确,并说明理由.
(1)延长直线AB;
(2)延长射线AB到C;
(3)延长线段AB到C.
分析:直线、射线、线段是最基本的几何图形之一.直线、射线、线段三者之间的联系表现为线段可以是射线和直线的一部分,射线可以是直线的一部分;它们的区别表现为三者的端点个数不同,端点的个数和位置就使三者具有不同的各向延伸性.由于直线都是可以向两方无限延伸的,所以延长直线AB是多余的,而“射线AB”就表示A为端点,向B的方向可以无限延伸,因而说法(2)也是错误的.而只有线段有两个端点,可以任意向任意一方延伸,所以(3)是正确的.
在初学平面几何时,一定要注意用文字、符号表达的概念与图形之间的内在联系.
例2 回答下列问题,并说明理由:
(1)如图1(甲)所示,直线AC和直线CA是不是同一条直线?射线AC和射线CA是不是同一条射线?射线BA和射线BC?射线AB和射线AC呢?
(2)如图1(乙),线段MN的延长线是什么?线段NM的延长线呢?线段NM的反向延长线呢?

分析:射线和线段都是用直线被点分成的部分来定义的,定义是对图形的分析、比较得出的,解答此类问题的主要方法仍然是抓住几何概念所反映的几何图形的本质属性.
解:(1)直线AC和直线CA都是经过AC两点的直线,根据过两点有且只有一条直线可知,它们是同一条直线.
射线AC是直线AD上点A右边的部分,而射线CA是直线AD上点C左边的部分,这两条射线的端点不同,延伸的方向也不同,根据射线的定义可知,它们不是同一条射线.
射线BA和射线BC虽然具有相同的端点,但是BA和BC字母的排列与图形反映的相应点的位置揭示它们具有不同的延伸方向,根据射线的定义,它们也不是同一条射线.
射线AB和射线AC,具有相同的端点,又都有相同的伸展方向,都表示直线AD上点A右边的部分,所以,它们是相同的射线.
(2)根据线段的延长线的定义可知,线段MN的延长线是射线MP;线段NM的延长线是射线NO;线段NM的反向延长线就是把线段NM向着它相反的方向延伸所得到的射线,实际上就是线段MN的延长线,即射线MP.
例3 如图2所示,4种情况下的直线、射线或线段可能相交的是哪几个.
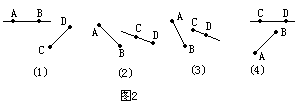
解:图2(1)中,AB是直线,它可以向两个方向无限伸展,从图中的位置来看,直线AB与CD一定相交.
在图2(2),(3)中,AB是线段,而DC,CD都是射线,但是延伸的方向不同,图2(2)中射线DC向左延伸一定和AB相交,而图2(3)中的射线CD向右延伸与线段AB不能相交.
图2(4)中的直线CD虽然可以向两个方向延伸,但是图中所处的位置决定它与不能向任何方向延伸的线段AB没有交点.
与图形相关的概念、性质以及图中各种图形的相关位置是判断的主要依据.
例4 判下列说法是否正确,并说明理由:
(1)在所有连结两点的线中,直线最短;
(2)两点之间,线段最短;
(3)画出A、B两点间的距离;
(4)连结两点的线段叫做两点间的距离.
解:(1)不正确,因为直线是一个图形,它可以向两方无限延伸,它没有长度,同时“连结”一词专用在连成线段,用于两点之间各种形状的线,应用“联接”.
(2)正确,所有联接两点的线中,线段最短,也可简单说成:两点之间,线段最短.
(3)不正确,根据两点间的距离的定义可知,两点间的距离是一个数量,它不是图形,不能把它画出来.
(4)不正确,连结两点的线段的长度才是两点间的距离.
线段和它的长度,一个是图形,一个是数量,在初学几何时,一定要注意到“几何语言”的正确性.
二、几何概念与对应图形的相互转换
认识几何图形与概念教学是密不可分的.从各种不同的角度强化图形与概念之间的相互转换是十分重要的.在平面几何学习的初始阶段,这种转换的训练大致有以下两个方面:其一,“看图说话”,用文字语言、符号语言说明给出的图形,根据图形进行概念之间的辨析、确定、进行分析,思考;其二:“读话画图”,根据文字语言,符号语言所表示的命题,句子,画出相应的图形.
例5 平面上有任意3个点A,B,C.问:
(1)一共可以画出多少条直线?
(2)以一点为端点且经过另一点的射线可以得到多少条?
(3)可以得到多少条线段?
分析:射线、线段都是直线的一部分,因而首先必须考虑可以画出多少条直线,由于经过两点有且只有一条直线,所以必须知道3点中每两点组成一组,一共可以组成多少个组.另一方面,已知3点的位置是任意的,就是说,这3点的位置是不确定的.我们先由其中两点(如A、B)画出一条直线AB,那么C点与直线AB的位置关系就只有两种:点C在直线AB上或点C不在直线AB上,在这两种情况下,所得到直线的条数也是不一样的.考虑了直线的条数,在此基本上就可以得到射线和线段的条数.
解:经过A、B两点可以画一条直线,则点C与直线AB的位置关系有:
(1)点C在直线AB上(如图3)显然直线CA、CB与直线AB是同一条直线,因此在这种情况下可以画出一条直线.
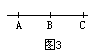
由于A,B,C在同一条直线上,以最左端一点A为端点而经过B点、C点的射线有两条AB、AC,但这两条射线实际上是同一条射线,同样以最右端的一点C为端点的射线CB,CA也是同一条射线,只有以中间一点B为端点的两条射线BA,BC由于延伸方向不同,是不同的两条射线,所以,可以得到4条射线.
同样,根据线段的定义,如果A,B,C在同一直线上,可以得到3条不同的线段AB,BC,CA.
(2)点C不在直线AB上,(如图4)根据过两点有且只有一条直线可以画出3条直线:AB,BC,CA.
而以A点为端点的射线有4条,其中只有两条分别经过点B,点C,所以,以A为端点的满足条件的射线有两条AB,AC.同理,以点B,以点C为端点的射线也分别有两条满足条件.所以一共可以画6条射线:AB,AC;BA,BC;CA,CB.
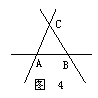
以A、B、C3点为端点的线段仍然有3条.
综合上述,给出平面上的任意3点,可以得到一条或3条直线;4条或6条以一点端点而经过另一点的射线;不论3点的相互位置如何,总可以得到3条线段.
例6 已知线段a,b(a>b),用直尺和圆规画出线段x,线段y,使:(1)x=a+2b;(2)y=3a-2b.
分析:“读话画图”,首先要了解画图的一些基本方法,在头脑中形成一个很有条理的程序,这个程序记录下来就是画法.作“线段的和、差”是最基本的作图,它有自己的画法程序及作图语言,以(1)为例,画图步骤为:
①画射线AE;
②用圆规在射线AE上顺次截取AB=a,BC=CD=b(图5).

线段AD就是所求的线段x.
为什么采取这样的画图程序呢?因为要作一条线段,主要是决定线段的位置以及线段的两个端点的位置,在画法的第一步“画射线AE”就是确定了所求线段的位置,线段x在射线AE上,并且决定了第1个端点A的位置,但是第2个第3个第4个端点就不能任意取了,必须保证最后得到的线段总长度是a+2b,所以第二步的画法是“在射线AE上顺次截取AB=a,BC=CD=b”,“顺次”一词,就表示线段是一个挨着一个地截取.
同样第(2)题的画法为(如图6):
![]()
①画射线EQ;
②在射线EQ上顺次截取EF=FG=GH=a;
③在线段HE上顺次截取HI=IP=b.
线段EP就是所要画的线段y.
三、借助数量进行图形的度量和比较
比较两条线段的长短,可以把它们移到同一条直线上,并使两条线段从同一个端点出发,根据另一端点的位置进行比较,这是几何的本身特点.在给出线段的度量方法后,线段的比较及和差倍的计算又可以借助数量来进行,两者的一致性,使数和形紧密地结合在一起.
例7 已知线段AB=5cm,延长AB到C,使AC=7cm,在AB的反向延长线上取D,使BD=4BC,设线段CD的中点为E.问,线段AE是线段CD的几分之一.
分析:根据题意作出示意图(如图7),从图中可以看到“延长AB到C,使AC=7cm”,所延长的线段就是BC,很显然BC=AC-AB=2cm,由此,就可以求得BD,DC的长,再根据E为CD中点,求得AE的长.
![]()
解:∵AC=AB+BC,即7=5+BC,
∴BC=2(cm).
∵BD=4BC,即BA+AD=4BC,5+AD=8,
∴AD=3(cm),
∴CD=AD+AB+BC=3+5+2=10.
∵E为CD的中点,
∴DE=5,即AD+AE=5,即3+AE=5,
∴AE=2(cm),
![]()
解此类问题,一般先按题意画出示意图,再根据图示的情况确定所求线段和已知线段的关系,从而得出所求线段的长.
例8 将线段AB延长到C,使BC=2AB,AB的中点为D,E、F是BC上的点,且BE∶EF=1∶2,EF∶FC=2∶5,AC=60cm,求DE,DF的长.
![]()
分析:从示意图(图8)中,我们得到了D,E,F点的大致位置,它们之间的度量关系却借助数量关系的分析.在众多的线段中,发现BE的长度是最基本的,知道了它的数量,其余线段的长度都可以求得,因此我们选择BE作为基本量,列出一系列的关系式.
解:设BE=k,
∵BE∶EF=1∶2,
∴EF=2k;
又EF∶FC=2∶5,
∴FC=5k,
∵BC=BE+EF+FC,BC=2AB,
∴BC=8k,AB=4k.
∴AC=AB+BC=60cm,即12k=60,
∴k=5(cm).
![]()
∴DE=DB+BE=3k=15(cm),
DF=DE+EF=5k=25(cm).
例9 一条直线上顺次有A,B,C,D4点,C为AD的中![]()
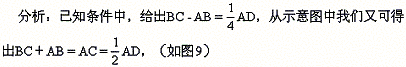
![]()
如果都用AD来表示BC,AB,就可以得出它们的数量关系.为表达方便,可以采用代数的方法,列出相应的方程组.
解:设AB=x,BC=y,AD=z.


