第一节 平面直角坐标系

典型例题

　　例1、如图写出A、B、C、D、E、F、O各点的坐标．

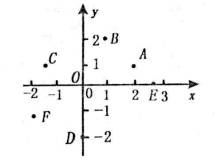
　　分析：求点A的坐标，由点A向x轴作垂线，垂足在x轴上的坐标2就是点A的横坐标；由点A向y轴作垂线，垂足在y轴上的坐标1就是点A的纵坐标．按横坐标2在前，纵坐标1在后的顺序，用逗号隔开写在小括号内，即可得点A的坐标是（2，1）．同理可得到点B、C、D、E、F、O的坐标．

　　解：点A、B、C、D、E、F、O的坐标分别是
　　

　　说明：点A和点Ｂ的坐标学生有可能会认为是相同的，教师应加以矫正．

　　例2、在平面直角坐标系内描出下列各点，并指出它们所在的象限或坐标轴：

　　

　　分析：根据点A的坐标（3，2）来确定A的位置，先要在x轴上找到表示3的点，过这点作x轴的垂线；再在y轴上找到表示2的点，过该点再y轴的垂线，两垂线的交点为点A．同理可以找到点B、C、D、E、F、G的位置，从而描出各点，再根据它们的位置写出所在象限或坐标轴.

　　

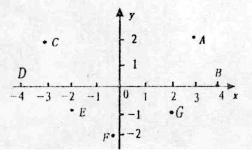
　　解：点A、B、C、D、E、F、G的位置如上图.

　　点A在第一象限，点B在x轴上，点C在第二象限，点D在x轴上，点E在第三象限点F在y轴上，点G在第四象限.

　　说明：x轴、y轴把坐标平面分成四个象限，坐标轴上的点不在任何一个象限内.

　　例3、选择题：

　　（1）点M（5，－6）关于x轴的对称点的坐标是（ ）．

　　（A）（－6，5）　　　（B）（－5，－6）

　　（C）（5，6）　　　　（D）（－5，6）

　　（2）点N（a，-b）关于原点的对称点是坐标是（ ）.

　　（A）（-a，b）　　　（B）（-a，-b）

　　（C）（a，b）　　　　（D）（-b，a）

　　解：（1）把点M（5，-6）和选项中的四个点都描在同一坐标系内，可发现只有点（5，6）和M点关于x轴对称，因此选C．

　　另法：点M（5，-6）在第四象限，和点Ｍ关于x轴对称的点应在第一象限，选项中只有点（5，6）在第一象限，因此选C．

　　方法三：两个点关于x轴对称，它们的横坐标相同，纵坐标互为相反数，反之也对．在选项中的四个点，只有点（5，6）符合题意．因此选C．

　　（2）两个点关于原点对称，它们的横坐标互为相反数，纵坐标也互为相反数，反之也对．选项中只有点（-a，b）符合题意，因此选A．

　　另法：或令a＝1，b＝1，则Ｎ点的坐标为（1，－1）在第四象限，和Ｎ关于原点对称的点应在第二象限，其坐标为（-1，1）只有（-a，b）合题意，因此选A．

　　例4、（1）若点A（a，b）在第三象限，则点Q（-a+1，3b-5）在第________象限；

　　（2）若点B（m+4，m-1）在x轴上，则m=_____________.

　　（3）若点C（x，y）满足x+y＜0，xy＞0，则点C在第___________象限.

　　（4）若点D（6-5m，m²-2）在第二、四象限夹角平分线上，则m=_________.

　　（5）已知点 和点 关于y轴对称，则a=______，b=________.

　　解：（1） 点A（a，b）在第三象限

　　　

　　　 点Q（-a+1，3b-5）在第四象限

　　（2） 点B（m+4，m-1）在x轴上

　　　

　　（3） xy＞0， 同号

　　　 x+y＜0， 均为负.

　　　 点C在第三象限.

　　（4） 点D（6-5m，m²-2）在第二、四象限夹角平分线上，

　　　

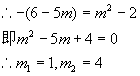
　　（5） 点 和点 关于y轴对称，

　　　

　　说明：这组填空题是点的坐标特征的应用，要记住点在四个象限内的符号特征，点在坐标轴上，一，三与二，四象限夹角平分线上的特征；点关于x轴，y轴，原点对称点的特征.

　　例5、如图， 的边长 ，若把它放在直角坐标系内，是AB在x轴上，点C在y轴上，如果A的坐标是（-3，0），求B、C、D的坐标.

　　

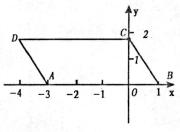
　　分析：求点的坐标，应由该点向x轴、y轴作垂线，根据垂足的坐标来定点的坐标.而垂足的坐标应结合 的边长来确定，先确定垂足到原点的距离，再根据点的位置来确定坐标的符号.

　　解： 设点B坐标为（b，0），

　　　

　　　 标为（1，0）

　　　设点C的坐标为（0，c），由OB=1，BC=2，

　　　得

　　　 ，于是点C的坐标为

　　　设点D的坐标为

　　　作 轴于 ，易证

　　　即

　　　于是，D点坐标为

　　　从而点B、C、D的坐标分别为（1，0）， 和

　　例6、如果点A（0，0），B（3，0），点C在y轴上，且 的面积是5，求C点坐标.

　　解：设点C坐标为（0，y），
　　　
　　　
　　　即
　　　于是点C的坐标为

　　说明：用点的坐标差的绝对值来表示线段长度的化简过程中，应根据绝对值的意义来决定取正数、负数或者零.如例4中点C（0，c）在原点上方，所以c＞0，于是 ；点 在原点左侧，所以d＜0，于是 如果点的位置不确定，无法判断坐标的大小，化简时就应分情况讨论，如例5中点C（0，y）在y轴上，但不知在原点的上方还是下方，不能判断y与0的大小，因此，化简 时，得 .

返回页首　　

典型例题

　　例1、下面的表分别给出了变量x与y之间的对应关系，判断y是x的函数吗？如果不是，说明出理由.

	1	2	3	4	5
	3	6	9	12	15
	1	2	3	4	5
	7	11	8	12	15
	1	2	3	2	1
	2	5	10	-5	-2
	1	2	3	4	5
	9	9	9	9	9

　　解：（1）y是x的函数；

　　（2）y是x的函数；

　　（3）y不是x的函数，因为对于变量x=1，变量y有1与-1两个值与它对应；

　　（4）y是x的函数

　　说明：对于x的每一个值，y都有唯一的值与它对应.第四个是常数函数它符合函数的定义.

　　例2、判断下列关系是不是函数关系？

　　（1）长方形的宽一定时，其长与面积；

　　（2）等腰三角形的底边长与面积；

　　（3）某人的年龄与身高；

　　（4）关系式| y |=x中的y与x.

　　分析：判断一个关系是不是函数关系，第一要看是不是一个变化过程；第二要看在这个变化过程中，是不是有两个变量；第三要看自变量每取一个确定值，函数是不是都有唯一确定的值与它对应.

　　解：（1）长方形的宽一定时，其长所取的每一个确定的值，面积都有唯一确定的值与它对应，所以长与面积是函数关系.

　　（2）因为三角形的面积受底和高两个因素的影响，当等腰三角形的底取一个定值时，它的面积又受高的影响，不能有唯一确定的值和底相对应，所以底边长与面积不是函数关系.

　　（3）人的任意一个确定的年龄，都有唯一确定的身高与之相对应，所以某人的年龄与身高是函数关系.

　　（4）x每取一个正值，y都有两个值与它对应，所以| y | = x不是函数关系.

　　说明：年龄与身高的变化不按某种规律，但某人每一个确定的年龄，必有唯一确定的身高和   它相对应，因此函数关系是一定的，所以不要以为存在一定比例关系或一定规律，能用解析式表示的才是函数关系.

　　例3、汽车由北京驶往相距850千米的沈阳，它的平均速度为80千米/小时，求汽车距沈阳的路程S（千米）与行驶时间t（小时）的函数关系式，写出自变量的取值范围.

　　分析：北京距沈阳850千米，汽车距沈阳的路程等于全程减去已行驶的路程，已行驶的路程等于速度乘以时间.

　　解：

　　　

　　　得

　　　

　　于是汽车距沈阳的路程S与时间t的函数关系式为 ，自变量t的取值范围是

　　例4、求下列函数中自变量x的取值范围：

　　（1） 　（2）

　　（3） 　（4）

　　（5） 　（6）

　　（7） 　（8）

　　分析：求自变量的取值范围，应考虑自变量的取值使函数解析式有意义.（1）、（2）小题函数解析式是整式，故自变量可取任意实数；（3）、（4）小题解析式是分式，自变量可取使分母不为0的任意实数；（5）、（7）、（8）小题的解析式是二次根式，自变量取值应使被开方数非负；（6）小题既有分母又有二次根式，自变量取值应使分母不为0，又要使二次根式的被开方数非负.

　　解：（1）函数 的自变量x的取值范围是躯体实数

　　（2）函数 的自变量x的取值范围是躯体实数

　　（3）

　　　 当 时，分母 ，

　　　 函数 的自变量的取值范围是 ；

　　（4）由 解得

　　　 当 或 时，分母 ，

　　　 函数 的自变量x 的取值范围是 且

　　（5）由 解得 ，

　　　 函数 的自变量x的取值范围是 ；

　　（6）由 得 ，由 得 ，当 时，分母 ，

　　　 函数 的自变量x的取值范围是 且 ；

　　（7）

　　　即对于任意实数x， 都是非负的，

　　　   函数 的自变量x的取值范围是全体实数；

　　（8）由 得

　　因此，函数 的自变量x的取值范围是 .

返回页首