 设为首页
设为首页
 加入收藏
加入收藏
教学设计示例(一)
任意角的三角函数
教学目标:
1.通过对初中锐角三角函数定义的回忆,掌握任意角三角函数的定义法,并掌握用单位圆中的有向线段表示三角函数值.
2.掌握已知角 ![]() 终边上一点坐标,求四个三角函数值.(即给角求值问题)
终边上一点坐标,求四个三角函数值.(即给角求值问题)
教学重点:
任意角的三角函数的定义.
教学难点:
任意角的三角函数的定义,正弦、余弦、正切这三种三角函数的几何表示.
教学用具:
直尺、圆规、投影仪.
教学步骤:
1.设置情境
角的范围已经推广,那么对任一角 ![]() 是否也能像锐角一样定义其四种三角函数呢?本节课就来讨论这一问题.
是否也能像锐角一样定义其四种三角函数呢?本节课就来讨论这一问题.
2.探索研究
(1)复习回忆锐角三角函数
我们已经学习过锐角三角函数,知道它们都是以锐角 ![]() 为自变量,以比值为函数值,定义了角
为自变量,以比值为函数值,定义了角 ![]() 的正弦、余弦、正切、余切的三角函数,本节课我们研究当角
的正弦、余弦、正切、余切的三角函数,本节课我们研究当角 ![]() 是一个任意角时,其三角函数的定义及其几何表示.
是一个任意角时,其三角函数的定义及其几何表示.
(2)任意角的三角函数定义
如图1,设 ![]() 是任意角,
是任意角, ![]() 的终边上任意一点
的终边上任意一点 ![]() 的坐标是
的坐标是 ![]() ,当角
,当角 ![]() 在第一、二、三、四象限时的情形,它与原点的距离为
在第一、二、三、四象限时的情形,它与原点的距离为 ![]() ,则
,则 ![]() .
.
定义:①比值 ![]() 叫做
叫做 ![]() 的正弦,记作
的正弦,记作 ![]() ,即
,即 ![]() .
.
②比值 ![]() 叫做
叫做 ![]() 的余弦,记作
的余弦,记作 ![]() ,即
,即 ![]() .
.
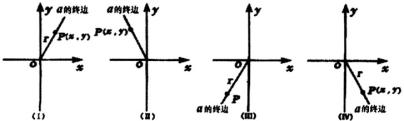
图1
③比值 ![]() 叫做
叫做 ![]() 的正切,记作
的正切,记作 ![]() ,即
,即 ![]() .
.
同时提供显示任意角的三角函数所在象限的课件
提问:对于确定的角 ![]() ,这三个比值的大小和
,这三个比值的大小和 ![]() 点在角
点在角 ![]() 的终边上的位置是否有关呢?
的终边上的位置是否有关呢?
利用三角形相似的知识,可以得出对于角 ![]() ,这三个比值的大小与
,这三个比值的大小与 ![]() 点在角
点在角 ![]() 的终边上的位置无关,只与角
的终边上的位置无关,只与角 ![]() 的大小有关.
的大小有关.
请同学们观察当 ![]() 时,
时, ![]() 的终边在
的终边在 ![]() 轴上,此时终边上任一点
轴上,此时终边上任一点 ![]() 的横坐标
的横坐标 ![]() 都等于0,所以
都等于0,所以 ![]() 无意义,除此之外,对于确定的角
无意义,除此之外,对于确定的角 ![]() ,上面三个比值都是惟一确定的.把上面定义中三个比的前项、后项交换,那么得到另外三个定义.
,上面三个比值都是惟一确定的.把上面定义中三个比的前项、后项交换,那么得到另外三个定义.
④比值 ![]() 叫做
叫做 ![]() 的余切,记作
的余切,记作 ![]() ,则
,则 ![]() .
.
⑤比值 ![]() 叫做
叫做 ![]() 的正割,记作
的正割,记作 ![]() ,则
,则 ![]() .
.
⑥比值 ![]() 叫做
叫做 ![]() 的余割,记作
的余割,记作 ![]() ,则
,则 ![]() .
.
可以看出:当 ![]() 时,
时, ![]() 的终边在
的终边在 ![]() 轴上,这时
轴上,这时 ![]() 的纵坐标
的纵坐标 ![]() 都等于0,所以
都等于0,所以 ![]() 与
与 ![]() 的值不存在,当
的值不存在,当 ![]() 时,
时, ![]() 的值不存在,除此之外,对于确定的角
的值不存在,除此之外,对于确定的角 ![]() ,比值
,比值 ![]() ,
, ![]() ,
, ![]() 分别是一个确定的实数,所以我们把正弦、余弦,正切、余切,正割及余割都看成是以角为自变量,以比值为函数值的函数,以上六种函数统称三角函数.
分别是一个确定的实数,所以我们把正弦、余弦,正切、余切,正割及余割都看成是以角为自变量,以比值为函数值的函数,以上六种函数统称三角函数.
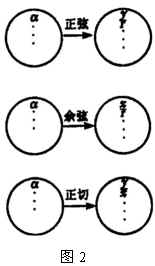 (3)三角函数是以实数为自变量的函数
(3)三角函数是以实数为自变量的函数
对于确定的角 ![]() ,如图2所示,
,如图2所示, ![]() ,
, ![]() ,
, ![]() 分别对应的比值各是一个确定的实数,因此,正弦,余弦,正切分别可看成从一个角的集合到一个比值的集合的映射,它们都是以角为自变量,以比值为函数值的函数,当采用弧度制来度量角时,每一个确定的角有惟一确定的弧度数,这是一个实数,所以这几种三角函数也都可以看成是以实数为自变量,以比值为函数值的函数.
分别对应的比值各是一个确定的实数,因此,正弦,余弦,正切分别可看成从一个角的集合到一个比值的集合的映射,它们都是以角为自变量,以比值为函数值的函数,当采用弧度制来度量角时,每一个确定的角有惟一确定的弧度数,这是一个实数,所以这几种三角函数也都可以看成是以实数为自变量,以比值为函数值的函数.
即:实数→角(其弧度数等于这个实数)→三角函数值(实数)
(4)三角函数的一种几何表示
利用单位圆有关的有向线段,作出正弦线,余弦线,正切线,如下图3.
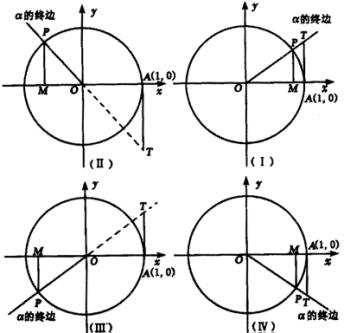
图3
设任意角 ![]() 的顶点在原点
的顶点在原点 ![]() ,始边与
,始边与 ![]() 轴的非负半轴重合,终边与单位圆相交于点
轴的非负半轴重合,终边与单位圆相交于点 ![]() ,过
,过 ![]() 作
作 ![]() 轴的垂线,垂足为
轴的垂线,垂足为 ![]() ;过点
;过点 ![]() 作单位圆的切线,这条切线必然平行于轴,设它与角
作单位圆的切线,这条切线必然平行于轴,设它与角 ![]() 的终边(当
的终边(当 ![]() 为第一、四象限时)或其反向延长线(当
为第一、四象限时)或其反向延长线(当 ![]() 为第二、三象限时)相交于
为第二、三象限时)相交于 ![]() ,当角
,当角 ![]() 的终边不在坐标轴上时,我们把
的终边不在坐标轴上时,我们把 ![]() ,
, ![]() 都看成带有方向的线段,这种带方向的线段叫有向线段.由正弦、余弦、正切函数的定义有:
都看成带有方向的线段,这种带方向的线段叫有向线段.由正弦、余弦、正切函数的定义有:
![]()
![]()
![]()
这几条与单位圆有关的有向线段 ![]() 叫做角
叫做角 ![]() 的正弦线、余弦线、正切线.当角
的正弦线、余弦线、正切线.当角 ![]() 的终边在
的终边在 ![]() 轴上时,正弦线、正切线分别变成一个点;当角
轴上时,正弦线、正切线分别变成一个点;当角 ![]() 的终边在
的终边在 ![]() 轴上时,余弦线变成一个点,正切线不存在.
轴上时,余弦线变成一个点,正切线不存在.
(5)例题讲评
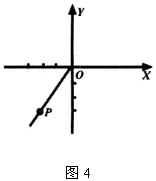 【例1】已知角
【例1】已知角 ![]() 的终边经过
的终边经过 ![]() ,求
,求 ![]() 的六个三角函数值(如图4).
的六个三角函数值(如图4).
解:∵ ![]()
![]()
∴ ![]()
![]()
![]()
![]()
![]()
![]()
![]()
提问:若将 ![]() 改为
改为 ![]()
![]() ,如何求
,如何求 ![]() 的六个三角函数值呢?(分
的六个三角函数值呢?(分 ![]() ,
, ![]() 两种情形讨论)
两种情形讨论)
【例2】求下列各角的六个三角函数值
(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
解:(1)∵当 ![]() 时,
时, ![]() ,
, ![]()
∴ ![]() ,
, ![]() ,
, ![]()
![]() 不存在,
不存在, ![]() ,
, ![]() 不存在
不存在
(2)∵当 ![]() 时,
时, ![]() ,
, ![]()
∴ ![]() ,
, ![]()
![]() 不存在
不存在 ![]()
![]() 不存在
不存在 ![]()
(3)当 ![]() 时,
时, ![]() ,
, ![]()
∴ ![]()
![]()
![]()
![]() 不存在
不存在 ![]()
![]() 不存在
不存在
【例3】作出下列各角的正弦线,余弦线,正切线.(1) ![]() ;(2)
;(2) ![]() .
.
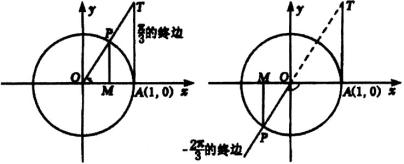
解: ![]() ,
, ![]() 的正弦线,余弦线,正切线分别为
的正弦线,余弦线,正切线分别为 ![]() .
.
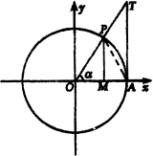 【例4】求证:当
【例4】求证:当 ![]() 为锐角时,
为锐角时, ![]() .
.
证明:如右图,作单位圆,当 ![]() 时作出正弦线
时作出正弦线 ![]() 和正切线
和正切线 ![]() ,连
,连 ![]()
∵ ![]()
∴ ![]()
![]()
![]()
∴ ![]()
利用三角函数线还可以得出如下结论
![]() 的充要条件是
的充要条件是 ![]() 为第一象限角.
为第一象限角.
![]() 的充要条件是
的充要条件是 ![]() 为第三象限角.
为第三象限角.
练习(学生板演,利用投影仪)
(1)角 ![]() 的终边在直线
的终边在直线 ![]() 上,求
上,求 ![]() 的六个三角函数值.
的六个三角函数值.
(2)角 ![]() 的终边经过点
的终边经过点 ![]() ,求
,求 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(3)说明 ![]() 的理由.
的理由. ![]() .
.
解答:
(1)先确定终边位置
①如 ![]() 在第一象限,在其上任取一点
在第一象限,在其上任取一点 ![]() ,
, ![]() ,则
,则
![]() ,
, ![]()
![]()
![]()
![]()
![]()
②如 ![]() 在第三象限,在终边上任取一点
在第三象限,在终边上任取一点 ![]()
![]() ,则
,则
![]() ,
,
![]()
![]()
![]()
![]()
![]()
(2)若 ![]() ,不妨令
,不妨令 ![]() ,则
,则 ![]() 在第二角限
在第二角限 ![]()
∴ ![]()
![]()
![]()
![]()
(3)在 ![]() 终边上任取一点
终边上任取一点 ![]() ,因为
,因为 ![]() 与
与 ![]() 终边相同,故
终边相同,故 ![]() 也为角
也为角 ![]() 终边上一点,所以
终边上一点,所以 ![]() 成立.
成立.
说明:以后会知道,求三角函数值的方法有多种途径.用定义求角 ![]() 的三角函数值,是基本方法之一.当角终边不确定时,要首先确定终边位置,然后再在终边上取一个点来计算函数值.
的三角函数值,是基本方法之一.当角终边不确定时,要首先确定终边位置,然后再在终边上取一个点来计算函数值.
3.反馈训练
(1)若角 ![]() 终边上有一点
终边上有一点 ![]() ,则下列函数值不存在的是( ).
,则下列函数值不存在的是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(2)函数 ![]() 的定义域是( ).
的定义域是( ).
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
(3)若 ![]() ,
, ![]() 都有意义,则
都有意义,则 ![]() .
.
(4)若角 ![]() 的终边过点
的终边过点 ![]() ,且
,且 ![]() ,则
,则 ![]() .
.
参考答案:(1)D;(2)B;(3) ![]() 或8,说明点
或8,说明点 ![]() 在半径为
在半径为 ![]() 的圆上;(4)-6.
的圆上;(4)-6.
4.本课小结
利用定义求三角函数值,首先要建立直角坐标系,角顶点和始边要按既定的位置设置.角 ![]() 的三角函数定义式,其实是比例的化身,它的背后是相似形在支称着,不过这个定义具有一般性,如轴上角的三角函数,如果没有定义作为论据,欲求其函数性就不是很容易.
的三角函数定义式,其实是比例的化身,它的背后是相似形在支称着,不过这个定义具有一般性,如轴上角的三角函数,如果没有定义作为论据,欲求其函数性就不是很容易.
分类讨论(角位置)是三角函数求值过程中,使用频率非常高的一个数学思想,而分类标准往往是四个象限及四个坐标半轴.
课时作业:
1.已知角 ![]() 的终边经过下列各点,求角
的终边经过下列各点,求角 ![]() 的六个三角函数值.
的六个三角函数值.
(1) ![]() (2)
(2) ![]()
2.计算
(1)![]()
(2)![]()
(3)![]()
(4)![]()
3.化简
(1)![]()
(2)![]()
(3)![]()
(4)![]()
参考答案:
1.(1) ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]()
(2) ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]()
2.(1)-2;(2)8;(3)-1;(4) ![]()
3.(1)0;(2) ![]() ;(3)
;(3) ![]() ;(4)
;(4) ![]()
教学设计示例(二)
任意角的三角函数 第二课时
教学目标:
1.根据任意角三角函数定义,归纳出三角函数在各象限的符号,并能根据角 ![]() 的某种函数值符号,反馈出
的某种函数值符号,反馈出 ![]() 可能存在的象限.
可能存在的象限.
2.掌握诱导公式一,并能运用诱导公式把角 ![]() 的三角函数值转化为
的三角函数值转化为 ![]() 中角的三角函数值.
中角的三角函数值.
教学重点:
终边相同的角的同一三角函数值相等.
教学难点:
运用诱导公式把角 ![]() 的三角函数值转化为
的三角函数值转化为 ![]() 中角的三角函数值.
中角的三角函数值.
教学用具:
直尺、圆规、投影仪.
教学过程
1.设置情境
设角 ![]() 均是第二象限角,依三角函数定义,为了求
均是第二象限角,依三角函数定义,为了求 ![]() 的四个三角函数值,只要分别在
的四个三角函数值,只要分别在 ![]() 终边上取点
终边上取点 ![]() 、
、 ![]() ,由比值
,由比值 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,及
,及 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 可知,这两组比值虽然不一定相等,但由于
可知,这两组比值虽然不一定相等,但由于 ![]() 均在第二象限,故
均在第二象限,故 ![]() 同号,
同号, ![]() 同号,因而可见,
同号,因而可见, ![]() 的正弦、余弦、正切、余切值,符号是对应相同时。那么,当
的正弦、余弦、正切、余切值,符号是对应相同时。那么,当 ![]() 分别为一、三、四象限时,上述性质是否仍然成立呢?下面就可讨论这一问题.
分别为一、三、四象限时,上述性质是否仍然成立呢?下面就可讨论这一问题.
2.探索研究
(1)三角函数值的符号
今后我们还要经常用到三角函数在各个象限的符号,由于从原点到角的终边上任意一点的距离 ![]() 总是正值,根据三角函数定义可知,三角函数值符号取决于各象限内的坐标符号,请同学们分象限思考四个象限中三角函数值的符号.
总是正值,根据三角函数定义可知,三角函数值符号取决于各象限内的坐标符号,请同学们分象限思考四个象限中三角函数值的符号.
观察六个三角函数,可发现 ![]() 与
与 ![]() ,
, ![]() 与
与 ![]() ,
, ![]() 与
与 ![]() 互为倒数,因此它们的符号规律相同.
互为倒数,因此它们的符号规律相同.
![]() 当
当 ![]() 在第一、二象限时,
在第一、二象限时, ![]() ,
, ![]() ,所以
,所以 ![]() 为正,而当
为正,而当 ![]() 在第三、四象限时,
在第三、四象限时, ![]() ,
, ![]() ,
, ![]() 为负的.
为负的.
同理 ![]() 对于第一、四象限角是正的,而对于第二、三象限的角是负的.
对于第一、四象限角是正的,而对于第二、三象限的角是负的.
![]() 与
与 ![]() ,当
,当 ![]() 在第一、三象限时,
在第一、三象限时, ![]() 与
与 ![]() 同号,所以
同号,所以 ![]() ,
, ![]() ,而当
,而当 ![]() 在第二、四象限时,
在第二、四象限时, ![]() 与
与 ![]() 异号,
异号, ![]() ,
, ![]() .
.
现在我们将以上讨论结果整理成图1.
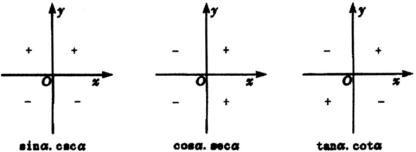
图1
可以表达为正弦和余割上正下负,余弦与正割左负右正,正切与余切一、三象限为正,二、四象限为负.同学们还可以自己用口诀“全正, ![]() 正,
正, ![]() 正,
正, ![]() 正”来记忆.
正”来记忆.
(2)诱导公式一
上节课我们已学过同终边的角,例如 ![]() 和
和 ![]() 都与
都与 ![]() 终边位置相同.
终边位置相同.
∵ ![]()
![]()
∴由三角函数定义可知它们的三角函数值相同,即
![]()
![]()
![]()
![]()
![]()
![]()
推广到一般情形,我们可得到诱导公式一:终边相同的角的同一三角函数值相等,即
|
|
这组公式的作用是可把任意角的三角函数值问题转化为0~360°角的三角函数值问题.
(3)例题分析
【例1】确定下列三角函数值符号:
(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]()
解:(1) ![]()
(2) ![]()
(3)∵ ![]() 是第四象限角,∴
是第四象限角,∴ ![]()
【例2】求证角 ![]() 为第三象限角的充分必要条件是
为第三象限角的充分必要条件是 ![]() ,
, ![]() .
.
证明:
必要性:当 ![]() 为第三象限角时,
为第三象限角时, ![]() ,
, ![]() ;
;
充分性:∵ ![]() 成立,∴
成立,∴ ![]() 角的终边可能位于第三或第四象限,也可以位于
角的终边可能位于第三或第四象限,也可以位于 ![]() 轴的非正半轴上;又∵
轴的非正半轴上;又∵ ![]() 成立,∴
成立,∴ ![]() 角的终边可能位于第一或第三象限,因为要同时成立,所以
角的终边可能位于第一或第三象限,因为要同时成立,所以 ![]() 角的终边只可能位于第三象限,于是角
角的终边只可能位于第三象限,于是角 ![]() 为第三象限角.
为第三象限角.
【例3】求下列三角函数值:
(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
解:(1)![]()
(2)![]()
(3)![]()
【例4】如果 ![]() 在第二象限,则
在第二象限,则 ![]() 的值是什么符号?
的值是什么符号?
解:∵ ![]() 在第二象限,∴
在第二象限,∴ ![]()
![]()
∴ ![]() ,
, ![]() ∴
∴ ![]()
【例5】若 ![]() 是第二象限的角,且
是第二象限的角,且 ![]() ,问
,问 ![]() 是第几象限角?
是第几象限角?
解:∵ ![]() 是第二角限的角,
是第二角限的角,
∴ ![]()
∴ ![]()
∴ ![]() 终边在第一或第三象限角,
终边在第一或第三象限角,
又∵ ![]() ∴
∴ ![]()
故 ![]() 是第三象限的角.
是第三象限的角.
【例6】求值: ![]()
解:原式
![]()
![]()
![]()
![]()
![]()
3.反馈练习
(1)已知 ![]() 是第三象限角且
是第三象限角且 ![]() ,则( )
,则( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(2)下列各式为正号的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
(3)若 ![]() 有意义,则
有意义,则 ![]() 是( )
是( )
A.第一象限角 B.第四象限角
C.第一或第四象限角 D.第一或第四或
![]() 轴正半轴
轴正半轴
(4)已知 ![]() 的终边过点
的终边过点 ![]() ,且
,且 ![]() ,
, ![]() ,则
,则 ![]() 的取值范围是_____.
的取值范围是_____.
(5)函数 ![]() 的值域是_____________.
的值域是_____________.
参考答案:(1)B;(2)C;(3)C;(4) ![]() ;(5)
;(5) ![]()
4.本课小结
(1)确定三角函数定义域时,主要应抓住三角函数定义中,比值的分母不得为零这一制约条件,当终边落在坐标轴上时,终边上任一点 ![]() 的坐标中,必有一分量为0,故相应有一比值无意义.
的坐标中,必有一分量为0,故相应有一比值无意义.
(2) ![]() 时,
时, ![]() ,
, ![]() 无意义,这两个函数定义域为
无意义,这两个函数定义域为 ![]()
课时作业:
1.确定下列三角函数值的符号
(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
(4)![]() (5)
(5) ![]() (6)
(6) ![]()
2.求值
(1) ![]()
(2) ![]()
参考答案:
1.(1)<0 (2)<0 (3)<0 (4)>0 (5)<0 (6)<0
(2)解:(1)原式 ![]()
![]()
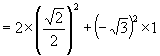
![]()
(2)原式 ![]()
![]()
![]()
![]()