 设为首页
设为首页
 加入收藏
加入收藏
典型例题(一)
例1 设有四个命题:
①底面是矩形的平行六面体是长方体;
②棱长都相等的直四棱柱是正方体;
③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;
④对角线相等的平行六面体是直平行六面体.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
分析:命题①是假命题.因为底面是矩形的直平行六面体才是长方体.底面是矩形,侧棱不垂直于底面,这样的四棱柱仍是斜平行六面体;
命题②是假命题.底面是菱形,底面边长与棱长相等的直四棱柱不是正方体;
命题③是假命题.因为有两条侧棱垂直于义面一边不能推出侧棱与底面垂直.
命题④是真命题,如图所示,平行六面体![]() 中所有对角线相等,对角面
中所有对角线相等,对角面![]() 是平行四边形,对角线
是平行四边形,对角线![]() ,所以四边形
,所以四边形![]() 是矩形,即
是矩形,即![]() ,同理四边形
,同理四边形![]() 是矩形,所以
是矩形,所以![]() ,由
,由![]() 知
知![]() 底面
底面![]() ,即该平行六面体是直平行六面体.
,即该平行六面体是直平行六面体.
故选A.
说明:解这类选择题的关键在于理清各种棱柱之间的联系与区别,要紧扣底面形状及侧棱与底面的位置关系来解题.
下面我们列表来说明平行四边形与平行六面体的性质的“类比”,由此,我们可以发现立体几何与平面几何许多知识是可以进行类比的.见表
表
| 平行四边形 |
平行六面体 |
| ①对边平行且相等 |
①相对的侧面平行且全等 |
| ②对角线交于一点,且在这一点互相平分 |
②对角线交于一点且在这一点互相平分 |
|
③四条边的平方和等于两条对角线的平方和 |
③十二条棱的平方和等于四条对角线的平方和 |
例2 如图,正四棱柱![]() 中,对角线
中,对角线![]() ,
,![]() 与侧面
与侧面![]() 所成角为
所成角为![]() ,求:(1)
,求:(1)![]() 与底面
与底面![]() 所成角;(2)异面直线
所成角;(2)异面直线![]() 与
与![]() 所成角;(3)正四棱柱的全面积.
所成角;(3)正四棱柱的全面积.
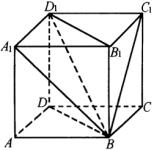 分析:正四棱柱是一种特殊的长方体,它的两底面
分析:正四棱柱是一种特殊的长方体,它的两底面![]() 、
、![]() 是正方形,长方体中有比较多的线面垂直关系,而线面垂直关系往往是解决立体几何问题的关键条件.题中无论是已知线面成角,还是求线面成角,都要把它们转化为具体的角,落实线面成角,先要找线面垂直关系.异面直线
是正方形,长方体中有比较多的线面垂直关系,而线面垂直关系往往是解决立体几何问题的关键条件.题中无论是已知线面成角,还是求线面成角,都要把它们转化为具体的角,落实线面成角,先要找线面垂直关系.异面直线![]() 与
与![]() 所成角通过
所成角通过![]() ,落实为具体的
,落实为具体的![]() .正四棱柱各个面都是矩形,求面积只要用矩形面积公式.
.正四棱柱各个面都是矩形,求面积只要用矩形面积公式.
解:(1)在正四棱柱![]() 中,
中,
∵![]() 面
面![]() ,
,
∴![]() 是
是![]() 与侧面
与侧面![]() 所成角,即
所成角,即![]() .
.
∵ ![]() ,∴
,∴ ![]() ,
,![]() ,
,
∵ ![]() 是正方形,∴
是正方形,∴![]() ,
,
![]() 平面
平面![]() ,∴
,∴ ![]() 是
是![]() 与底面
与底面![]() 所成角,
所成角,
在![]() △
△![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
即![]() 与底面
与底面![]() 所成角为
所成角为![]() .
.
(2)∵![]() ,
,
∴![]() 是
是![]() 与
与![]() 所成角(或补角).
所成角(或补角).
∵![]() 平面
平面![]() ,∴
,∴ ![]() ,
,
![]() △
△![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
即异面直线![]() 与
与![]() 所成角为
所成角为![]() .
.
(3)![]() △
△![]() 中,
中,![]() ,
,![]() .
.
∴ ![]() ,
,
∴ ![]() .
.
说明:长方体是一种特殊的棱柱,充分感受其中丰富的线面垂直、线线垂直关系是灵活解题的关键,各种垂直关系是解决立体几何中证明和计算的重要条件,可以看下面例子.
例3 如图,已知长方体![]() 中,棱长
中,棱长![]() ,
,![]() ,求直线
,求直线![]() 与平面
与平面![]() 的距离.
的距离.
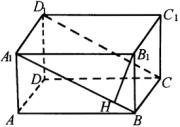 分析:求直线到平面的距离,首先要找直线上的点到平面的垂线,而找平面的垂线的一个很有用的思路是,找平面内一条直线与某一平面垂直,这里我们不难看出,长方体中有
分析:求直线到平面的距离,首先要找直线上的点到平面的垂线,而找平面的垂线的一个很有用的思路是,找平面内一条直线与某一平面垂直,这里我们不难看出,长方体中有![]() 平面
平面![]() ,这样,只要作
,这样,只要作![]() ,又有
,又有![]() ,得到
,得到![]() 平面
平面![]() .
.
解:长方体![]() 中,有
中,有![]() 平面
平面![]() ,过
,过![]() 作
作![]() 于
于![]() ,又有
,又有![]() ,
,
∴ ![]() 平
平![]() ,即
,即![]() 是
是![]() 到平面
到平面![]() 的距离.
的距离.
在![]() △
△![]() 中,由已知可得,
中,由已知可得,![]() ,
,![]() ,
,
∴ ![]() ,∴
,∴![]() .
.
即![]() 是
是![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.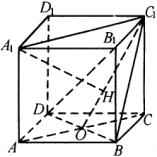
说明:长方体中有棱与面的线面垂直关系,正方体除此之外,还有对角线与对角面的线面垂直关系,比如,求正方体![]() 中,
中,![]() 与面
与面![]() 所成角.这里,要找
所成角.这里,要找![]() 与
与![]() 所成角,必须找
所成角,必须找![]() 到平面
到平面![]() 的垂线,因为
的垂线,因为![]() 面
面![]() ,在对角面
,在对角面![]() 内,过
内,过![]() 作
作![]() 于
于![]() ,则
,则![]() ,所以
,所以![]() 面
面![]() ,可以得到
,可以得到![]() 为
为![]() 与面
与面![]() 所成角,在对角面
所成角,在对角面![]() 中可计算
中可计算![]() .
.
例4 如图,已知直三棱柱![]() 中,
中,![]() ,
,![]() 为侧棱
为侧棱![]() 上一点,
上一点,![]() ,
,![]() .(1)若
.(1)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上不同于
上不同于![]() 、
、![]() 的任一点,求证:
的任一点,求证:![]() ;(2)若
;(2)若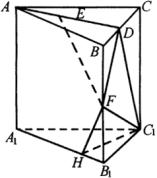
![]() ,求
,求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
分析:![]() 点在
点在![]() 上变化,
上变化,![]() 为平面
为平面![]() 内变化的一组相交直线(都过定点
内变化的一组相交直线(都过定点![]() ),要证明
),要证明![]() 与
与![]() 垂直,必有
垂直,必有![]() 平面
平面![]() .求
.求![]() 与平面
与平面![]() 所成角的关键是找
所成角的关键是找![]() 到面
到面![]() 的垂线,从而落实线面成角,直三棱柱中,侧棱
的垂线,从而落实线面成角,直三棱柱中,侧棱![]() 平面
平面![]() 给找点
给找点![]() 到面
到面![]() 的垂线创造了方便的条件.
的垂线创造了方便的条件.
解:(1)∵![]() ,且
,且![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又∵ 直三棱柱中![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴ ![]() 平面
平面![]() ,∴
,∴![]() .
.
在矩形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)过![]() 作
作![]() 于
于![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 平面
平面![]() ,连接
,连接![]() ,
,![]() 是
是![]() 与平面
与平面![]() 所成角.
所成角.
在等腰△![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,
在等腰△![]() 中,由面积相等可得,
中,由面积相等可得,![]() ,
,
∴![]() ,又
,又![]() ,
,
在![]() △
△![]() 中,
中,![]() ,
,
∴![]() ,
,
即![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
说明:由于点![]() 在
在![]() 上变化,给思考增加了难度,但仔细思考,它又提供了解题的突破口,使得线线垂直成为了
上变化,给思考增加了难度,但仔细思考,它又提供了解题的突破口,使得线线垂直成为了![]() 与一组直线垂直.本题的证明还有一个可行的思路,虽然
与一组直线垂直.本题的证明还有一个可行的思路,虽然![]() 在
在![]() 上变化,但是由于
上变化,但是由于![]() 平面
平面![]() ,所以
,所以![]() 点在平面
点在平面![]() 上的射影是定点
上的射影是定点![]() ,
,![]() 在平面
在平面![]() 上射影为定直线
上射影为定直线![]() ,使用三垂线定理,可由
,使用三垂线定理,可由![]() ,直接证明
,直接证明![]() .三垂线定理是转化空间线线垂直为平面内线线垂直的一个有力工具,再看一个例子,正方体
.三垂线定理是转化空间线线垂直为平面内线线垂直的一个有力工具,再看一个例子,正方体![]() 中,
中,![]() 是底面
是底面![]() 的中心,
的中心,![]() 是
是![]() 上动点,
上动点,![]() 是
是![]() 中点,求
中点,求![]() 与
与![]() 所成角.我们取
所成角.我们取![]() 中点
中点![]() ,虽然
,虽然![]() 点变化,但
点变化,但![]() 在面
在面![]() 上射影为定直线
上射影为定直线![]() ,在正方形
,在正方形![]() 中,易证
中,易证![]() ,所以,
,所以,![]() ,即
,即![]() 与
与![]() 所成角为
所成角为![]() .
.
典型例题(二)
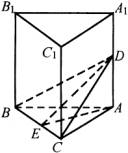 例5
如图,正三棱柱
例5
如图,正三棱柱![]() 的底面边长为4,侧棱长为
的底面边长为4,侧棱长为![]() ,过
,过![]() 的截面与底面成
的截面与底面成![]() 的二面角,分别就(1)
的二面角,分别就(1)![]() ;(2)
;(2)![]() 计算截面的面积.
计算截面的面积.
分析:要求出截面的面积,首先必须确定截面的形状,截面与底面成![]() 的二面角,如果
的二面角,如果![]() 较大,此时截面是三角形;但是如果
较大,此时截面是三角形;但是如果![]() 较小,此时截面与侧棱不交,而与上底面相交,截面为梯形.
较小,此时截面与侧棱不交,而与上底面相交,截面为梯形.
解:截面与侧棱![]() 所在直线交于
所在直线交于![]() 点,取
点,取![]() 中点
中点![]() ,连
,连![]() 、
、![]() ,
,
△![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∴![]() 为截面与底面所成二面角的平面角,
为截面与底面所成二面角的平面角,
∴![]() .
.
∵等边△![]() 边长为4,∴
边长为4,∴![]() .
.
在![]() △
△![]() 中,
中,![]() .
.
(1)当![]() 时,
时,![]() 点在侧棱
点在侧棱![]() 上,截面为△
上,截面为△![]() ,
,
在![]() △
△![]() 中,
中,![]() ,
,
 ∴
∴![]() .
.
(2)当![]() 时,
时,![]() 点在
点在![]() 延长线上,截面为梯形
延长线上,截面为梯形![]() ,
,
∵![]() ,
,![]() ∴
∴![]() 是△
是△![]() 的中位线,
的中位线,
∴![]() .
.
说明:涉及多面体的截面问题,都要经过先确定截面形状,再解决问题的过程,本例通过改变侧棱长而改变了截面形状,我们也可以通过确定侧棱长,改变截面与底面成角而改变截面形状.
 例6 斜三棱柱
例6 斜三棱柱![]() 中,平面
中,平面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)求![]() 与平面
与平面![]() 所成角;
所成角;
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小;
所成二面角的大小;
(3)求侧棱![]() 到侧面
到侧面![]() 的距离.
的距离.
分析:按照一般思路,首先转化条件中的面面垂直关系,由![]() ,取
,取![]() 的中点
的中点![]() ,连
,连![]() ,则有
,则有![]() ,从而有
,从而有![]() 平面
平面![]() ,在此基础上,
,在此基础上,![]() 与底面所成角以及平面
与底面所成角以及平面![]() 与底面所成二面角都能方便地找到,同时
与底面所成二面角都能方便地找到,同时![]() 底面
底面![]() 也为寻找
也为寻找![]() 点到面
点到面![]() 的垂线创造了条件.
的垂线创造了条件.
解:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() ,∴
,∴![]() ,∵平面
,∵平面![]() 底面
底面![]() ,
,
∴![]() 底面
底面![]() ,∴
,∴![]() 为
为![]() 与底面
与底面![]() 所成角.
所成角.
∵![]() 且
且![]() ,∴
,∴![]() .
.
(2)取![]() 中点
中点![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
连![]() ,∵
,∵![]() 底面
底面![]() ,∴
,∴![]() 在平面
在平面![]() 上射影为
上射影为![]() ,
,
∴![]() ,∴
,∴![]() 为侧面
为侧面![]() 与底面
与底面![]() 所成二面角的平面角.
所成二面角的平面角.
在等腰![]() △
△![]() 中,
中,![]() ,∴
,∴![]() .
.
在![]() △
△![]() 中,
中,![]() ,∴
,∴![]() .
.
在![]() △
△![]() 中,
中,![]() ,
,
∴![]() ,即侧面
,即侧面![]() 与底面
与底面![]() 所成二面角的大小为
所成二面角的大小为![]() .
.
(3)过![]() 作
作![]() 于
于![]() ,
,
∵![]() 底面
底面![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
在![]() △
△![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
说明:简单的多面体是研究空间线面关系的载体,而线面垂直关系又是各种关系中最重要的关系,立体几何中的证明与计算往往都与线面垂直发生联系,所以在几何体中发现并使用线面垂直关系往往是解题的关键,继续看下面例子.
例7 斜三棱柱![]() 的底面△
的底面△![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,
,![]() 在底面上的射影
在底面上的射影![]() 恰好是
恰好是![]() 的中点,侧棱与底面成
的中点,侧棱与底面成![]() 角,侧面
角,侧面![]() 与侧面
与侧面![]() 所成角为
所成角为![]() ,求斜棱柱的侧面积与体积.
,求斜棱柱的侧面积与体积.
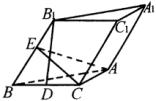 分析:
分析:![]() 在底面
在底面![]() 上射影
上射影![]() 为
为![]() 中点,提供了线面垂直
中点,提供了线面垂直![]() 平面
平面![]() ,另外又有
,另外又有![]() ,即
,即![]() ,又可以得到
,又可以得到![]() 平面
平面![]() ,利用这两个线面垂直关系,可以方便地找到条件中的线面角以及二面角的平面角.
,利用这两个线面垂直关系,可以方便地找到条件中的线面角以及二面角的平面角.
解:∵![]() 在底面
在底面![]() 上,射影
上,射影![]() 为
为![]() 中点.
中点.
∴![]() 平面
平面![]() .
.
∴![]() 为侧棱
为侧棱![]() 与底面
与底面![]() 所成角,即
所成角,即![]() ,
,
∵![]() ,即
,即![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,过
,过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() .
.
∴![]() 是侧面
是侧面![]() 与侧面
与侧面![]() 所成二面角的平面角,
所成二面角的平面角,
∴![]() ,
,
在直角△![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() ,
,
在直角△![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在直角△![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴侧面积为![]()
![]() .
.
体积为![]() .
.
说明:本例中△![]() 是斜棱柱的一个截面,而且有侧棱与该截面垂直,这个截面称为斜棱柱的直截面,我们可以用这个截面把斜棱柱分成两部分,并且用这两部分拼凑在一个以该截面为底面的直棱柱,斜棱柱的侧面积等于该截面周长乘以侧棱长,体积为该截面面积乘以侧棱长.
是斜棱柱的一个截面,而且有侧棱与该截面垂直,这个截面称为斜棱柱的直截面,我们可以用这个截面把斜棱柱分成两部分,并且用这两部分拼凑在一个以该截面为底面的直棱柱,斜棱柱的侧面积等于该截面周长乘以侧棱长,体积为该截面面积乘以侧棱长.