第七节 棱柱

祖冲之父子与祖暅原理

　　祖冲之（公元429—500年）是我国南北朝时代的伟大科学家，字文远，范阳郡蓟县（今河北省涞源县）人，祖父曾任朝庭的大匠卿，主管工程建筑．幼年常随祖父到工地参观，亲眼看到祖父的精心设计和工人们的辛勤劳动，幼小的心灵养成爱科学、爱技术、爱机械、爱劳动的习惯，20岁左右，受皇命入当时的最高学府—华林学省学习，结业后任南徐州从事史，后回建康（今南京）任过公府参军，以后做过晏县（今江苏昆山县东北）县令，后升为长水校尉．他钻研《九章算术》刘徽注之后，著有《缀述》附在刘徽注的后面，但遗憾的是这部著作已失传了．

　　祖冲之是天文学家，历学家，文学家、机械学家，数学家．说他是天文学家，历学家，是因为他创《大明历》；说他是文学家，是因为他著有《述异记》十卷；说他是机械学家，是因为他制造水碓、水磨，1000多年的今天，山区人们还在使用；说他是数学家，是因为他著《缀术》，虽书已失传，但其中对圆周率 的研究结果，以 为疏率、 为密率并求出 ，早于欧洲1100多年．以至于日本三上义夫在他所著的《中国数学发展史》中建议称圆周率为“祖率”．

　　祖暅是祖冲之的儿子，生卒年代不详，是一位博学多才的数学家．唐代王孝通称他为祖暅，阮元《畴人传》称他为祖暅之，另字景铄．他继承家学，主要工作是修补编辑他父亲的著述《缀述》，虽然他历官员外郎、散骑常侍．祖暅在数学上的主要成就，就是推算球的体积公式．在方法上根据他父亲提出的原理：“缘幂势既同，则积不容异”．其中幂指截面积，势指高，这一原理也可叙述为“两个等高的立体，若平行于底的截面积相等，则体积相等”．但在推算过程中祖暅却应用了“两个等高的主体，若平行于底的截面积成比例，则体积也成比例”更一般的结论，他的构思新颖．为了便于说明，先看下列三个图形：

　　图1是 球体，用 表示球体积．图2是 “牟合方盖”，用 表示“牟合方盖”体积．“牟合方盖”是一个特殊立体，是以 为直径的两个圆柱轴线垂直且相交而形成的．图3是以 为棱的正方体挖去一个倒立的阳马，用 表示其体积．

　　若用平行于底且相距为 的平面去截上述三个立体，所得截面面积分别为：

　　 ， ， ．

　　因为  ， ，

　　所以  ， ．

　　但从 可推得 ．

　　上述推算过程实际上图1起了桥梁作用，亦可从图3和图2直接推出：

　　因为 ，得 ．

　　所以由 就可推得 ．

　　祖暅在推算过程所应用的原理，西方叫卡瓦列利原理，因卡氏于公元1635年在《连续不可分量几何》里提出的，而这比祖冲之父子晚1100多年．因而我们将此原理称为“祖氏原理”或“祖暅原理”更为恰当．下面给出祖暅定理的两个推论，并利用原理及推论求椭圆的面积、椭球体的体积和环体体积．

　　推论1  夹在两个平行平面间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积比总为 ，那么这两个几何体的体积之比亦为 ，

　　推论2  夹在两条平行线间的两个平面图形，被平行于这两条平行线的任意直线所截，如果截得的两条线段之比总为 ，那么这两个平面图形的面积之比亦为 ．

　　问题1  求椭圆 的面积．

　　解  如图4，圆 方程为 ．作沿平行于 轴方向均匀压缩变换 代入圆 方程就得椭圆方程．由于椭圆与圆都夹在两条平行线 与 之间，且 ，由推论2得

                 ，

　　所以 ．

　　问题2  如图3，求以 轴为旋转，椭圆 为母线旋转生成的几何体体积．

　　解  以 为半径的圆面积为 ，以 为半径的圆面积为 ，则由推论2，得

　　 ，由推论1得 ，

　　所以   ．

　　一个圆绕同一平面内与它不相交的一条直线旋转形成的旋转面叫做环面，环面所围成的几何体叫做环体．

　　问题3  设圆 半径为 ，圆 绕它所在平面上与它不相交的直线 旋转，设点 到 的距离为 ，试求旋转所成的环体体积．

　　解  取一个底面半径为 高为 的圆柱和环体都平放在平面 上，则环体和圆柱都夹在两个平行平面之间．

　　用平行平面 的任意平面去截环体和圆柱，截面分别为圆环面和矩形面．设过圆 的圆心 及圆柱中心线且与 平面平行的平面 ，如果截平面与平面 的距离为 ，则截环体的得圆环面的外径为 ，内径为 ；截圆柱所得矩形的宽为 ，长为 ，

　　所以  圆环面积 ，

　　　　　矩形面积 ．

　　所以 ．

　　依祖暅原理，即

．

返回

高明的建筑—蜜蜂

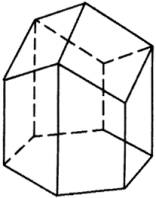　　 法国数学家傅里叶有句流传至今的名言：对自然的深入研究是数学发现的最富饶的源泉．黄金比是自然美的反映，蜂房问题也是极有趣的例子．蜂房的结构不仅有条理、有对称性，而且最省材料，这种“最省”实际上是极值问题．历史上不少学者注意到蜂房的奇妙结构．蜂房上有许多巢，取一个巢来看，它是正六角形的柱体，其上底是由三个全等的菱形组成（如图）．早在公元300年前后，亚历山大的巴普士就研究过蜂房的形状，他认为六棱柱的巢的结构是最经济的结构．开普勒曾说过这种充满空间的对称的蜂房的角应该和菱形 12面体（各个面都是菱形的12面体）的角一样．18世纪法国天文学家马拉尔弟经过实际测量后指出蜂巢顶部菱形的两角分别是 和 ．法国自然哲学家列俄木作出一个猜想，他认为用这样的角度来建造蜂房，在相同的容积下最节省材料．于是他请教瑞士数学家克尼希，克尼希证实了列俄木的猜想．但他通过数值计算推得：根据蜂房的构造法要使表面积最省料，其上底中菱形的两个角应为 和 ，和马拉尔弟实际测量的数值有 之着！当时人们认为：蜜蜂毕竟不懂科学，它们解决这样一个复杂的极值问题只有 的误差，是不足为奇的．可是事情还没有完结．后来，在调查一艘轮船失事原因的过程中，发现船上所使用的对数表有错误，而当时数学家克尼希进行蜂房计算时，所使用的也是同类对数表．于是，人们又开始怀疑克尼希计算数据的准确性．1743年，美国数学家马克劳林重新从理论上研究蜂巢中的极值问题，得到更惊人的结果．他完全用初等数学方法得到菱形的钝角是 ，锐角是 ，与实际测量的值一致．这 之差，不是蜜蜂不准，而是数学家克尼希算错了，他所用的对数表印错了．

　　马克思说得好：“蜜蜂建筑蜂房的本领使人间的许多建筑师感到惭愧．但是，最蹩脚的建筑师从一开始就比最灵巧的蜜蜂高明的地方，是他在用‘蜂蜡’建筑‘蜂房’以前，已经在自己的头脑中把它建成了．”

　　生物现象常常给人们很大启发，数学美是自然美的客观反映．

棱柱定义的发现学习

　　［课前准备工作：上课的一周前，发给每一个学生如图1、图2所示的展开图（比例尺5：1），让学生折成两个封闭的几何体．折成后的几何体如图3、图4．

　　这既是让学生动动手；也是为打开他们的思路与想象，预备了两个可能用得上的反例模型．]

　　1．这就是棱柱

　　上课了，教师随即演示如图5的各个棱柱的正例（至少演示三个）；并明确地说“这就是棱柱！”

　　让学生仔细观察后，教师设问：

　　T：我们所演示的几何模型的共同的本质属性是什么？即应怎样定义棱柱？

　　 ：（1）有两个面互相平行；（2）其余各面都是平行四边形，由这些面所围成的几何体叫做棱柱．

　　（这时，学生 的思维，属非逻辑思维，是一种合情推理．它代表了多数学生的看法．）

　　2．从质疑开始

　　教师请学生们拿出一周前发下做好的两个几何体，问：

　　T：我们所做的两个几何体是否满足了 归纳出的属性？但是，它们是柱形的吗，是否就是我们要定义的几何体？

　　学们都回答说：“所做的两个几何体满足 归纳的属性，但它们都不是棱柱．”

　　T：这表明， 的归纳错了．那么，是错在哪儿呢？是（1）有误；还是（2）有误；或者说，是归纳有缺漏之故，不完整．

　　［评：某结合存疑后，不忙于给予回答，先一一指出，“错在哪儿？”的几何可能—这也是重要的数学素质的训练．］

　　3．没有（1）行吗

　　T：没有（1）行吗？谁能以例子—几何模型来说明．

　　有学生举出如图6所示的几何体—从一个直棱柱中斜切一刀得来的，它没有任何两个面互相平行．

　　S：它不是棱柱．

　　T：这表明，没有属性（1）的几何体不是我们要定义的几何体．从而可知：（1）是本质属性．

　　4．没有（2）行吗？

　　T：那么，没有（2）行吗？我们也举出几何体来参与讨论，好吗？

　　……

　　教师帮助一下，演示如图7所示的几何体—两个面互相平行，其余各面不全是平行四边形，问“这说明什么问题？”

　　S：它也不是棱柱，不是我们正讨论的几何体．

　　T：这表明，棱柱的其余各面必须均为四边形（且均为平行四边形）．没有属性（2）也不行．那么，问题出在什么地方了呢？

　　5．看来是“属性表述不够完整了”

　　教师提醒学生，再次注意，已演示过的如图5及图3、4的几何体．

　　T：它们都满足 怕归纳出的两个属性，为什么一类是棱柱，另一类则不是，其间的差别在哪里？

教师又举出如图8所示的几何体，比较图5与图3、4、8后，学生发现：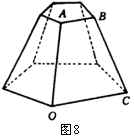

　　共同点是：其余各面都是四边形．

　　不同点是：图5中，每相邻的两个四边形的公共边都互相平行；而图3、4、8中的几何体，就不具有这个属性．

　　6．最后的定义

　　T：那么，请仔细分辨一下，这样定义棱柱合适吗？（教师展示小黑板）

　　有两个面互相平行，其余各面都是平行四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱．

　　……

　　T：这样的“定义”中，是否含有可导出属性—可导出属性，不是概念的本质属性，不能包含在此概念的定义之中．

　　这样，学生们终于发现：只要“其余各面都是四边形”就行．如图5， 等是本质属性， 等则是可导出的非本质属性．

　　带领学生，给出完整的定义，并作小结．

谈“两个对角面都是矩形的平行六面体一定是直平行六面体？”

　　对于命题“两个对角面都是矩形的平行六面体一定是直平行六面体”，文［l］通过给出两个有公共对角线 的全等矩形 ， ，构造出一个平行六面体 ，证明了该平行六面体不是直平行六面体，从而得出结论：该命题是一个假命题．笔者以为，文［l］的这个结论值得商榷．

　　文［1］所构造的平行六面体及证明其不是直平行六面体的过程无疑是正确的，问题是什么是平行六面体的对角向？

　　多面体中不在同一面上的三顶点所决定的平面称为多面体的对角面［2］．或表述为：多面体中含有一双对棱的平面或含有一棱及与它相对的顶点的平面，叫做这个多面体的对角面［3］．这是广义地对多面体的对角面所下的定义．文［l］显然是在这一定义下讨论的．但是，对于棱柱这种特殊的多面体，还有狭义的定义：对于棱柱（棱锥或棱台），经过不相邻的两条侧棱的截面叫做棱柱（棱锥或棱合）的对角面［4］．按照这种定义，原命题就是一个真命题．

　　两种定义，究意选择何种定义更适宜呢？笔者认为，在教学中它采用狭义的一种作为棱柱对角面的定义．这是因为：

　　1．棱柱作为一种特殊的多面体，为研究它的性质的方便，将其对角面的概念限制在经过个相邻的两条侧棱的截面的范围是必要的．如若不加这种限制，讨论棱柱（如六棱柱）的对角面的个数、形状及其面积的计算等，就显得很复杂，也难以为中学生所掌握，而加以限制后，棱柱、棱锥、棱台对角面的概念得到了统一，同时也容易得到：棱柱的对角面是平行四边形；直棱柱的对角面是矩形； 棱柱共有 （ ）个对角面；平行六面体有且只有两个对角面等等．

　　2．这种狭义的定义已被用于不少教科书中．如人民教育出版社出版的现行中等师范学校和普通中等专业学校《立体几何》教材以及上海科学出版社出版的数理化自学丛书《立体几何》等，使用的都是这一种定义．

　　3．尽管现行普通高中教材中没有出现对角面的定义，但在几乎所有的高中数学复习指导用书中，或者直接给出了这种狭义的定义，或者列出了以此定义为前提的性质：直棱柱的对角面都是矩形等．

　　4．也许有人会提出：平行六面体的底面不一定是水平放置的（图形变式），如果以文［1］中的 作底面， 不成了对角面吗？然而，此时面 的四条边均不能作为侧棱，即此时 不能作为对角面．

　　由此可知，棱柱对角面定义为“经过不相邻的两条侧棱的截面叫做棱柱的对角面”已是约定俗成并被普遍采用，而且棱柱对角面的性质已成为棱柱截面性质的一个有机组成部分．因此，在这种定义下，命题“两个对角面都是矩形的平行六面体一定是直平行六面体”不能认为是一个假命题．

参  考  文  献

　　l  刘毅．两个对角面都是矩形的平行六面体一定是直平行六面体？数学通讯，1997（8）

　　2  朱德祥．初等数学复习与研究（立体几何）．北京：人民教育出版社，1960

　　3  中学数学教师手册，上海：上海教育出版社，1986

　　4  数学小辞典．科学技术文献出版社，1983