 设为首页
设为首页
 加入收藏
加入收藏
例1.求函数![]() 的定义域.
的定义域.
分析:要求![]() ,即
,即![]() ,因为正弦函数具有周期性,所以只需先根据正弦曲线在一个周期上找出适合条件区间,然后两边加
,因为正弦函数具有周期性,所以只需先根据正弦曲线在一个周期上找出适合条件区间,然后两边加![]() .
.
解:由题意![]() ,
,
即 ![]() .
.
在一周期![]() 上符合条件的角为
上符合条件的角为![]() ,
,
∴定义域为![]()
![]() .
.
小结:解题时注意结合正弦曲线,而由于正弦函数的周期性,只需先在一个周期上求范围,这个周期的长度为![]() ,并非一定取
,并非一定取![]() ,而应该是否得到一个完整区间为标准,如本题若在
,而应该是否得到一个完整区间为标准,如本题若在![]() 上求范围则分为两段
上求范围则分为两段![]() 和
和![]() ,不如在
,不如在![]() 上是完整的一段.
上是完整的一段.
例2.求函数![]() 的定义域。
的定义域。
分析:上述函数从形式上看是一个较为复杂的复合函数,它是由三角函数、二次函数、对数函数复合而成。求定义域时,应分清脉络,逐一分析,综合得出结论。
解:欲求函数定义域,则由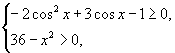
即![]() 也即
也即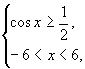
解得
取![]() 、0、1,可分别得到
、0、1,可分别得到
![]() 或
或![]() 或
或![]() 。
。
即所求的定义域为![]() 。
。
小结:在解本题时,容易出现的失误是,由![]() ,得
,得![]() 或
或![]() ;或在解不等式组
;或在解不等式组 时出现错误,如得出函数的定义域为
时出现错误,如得出函数的定义域为![]() 或
或![]() 等。
等。
解类似本例的问题,其关键在于求出两个或更多个不等式的公共解。而求公共解,如能借助于图形,由数形结合,往往可以事半功倍。具体方法一般可借助于数轴、单位圆或三角函数的图像来完成。如图甲、乙所示。
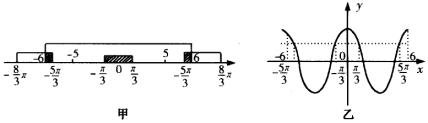
例3.求下列函数的值域:
(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() ; (4)
; (4)![]() .
.
分析:(1)先利用降幂公式,将其化为一个角的一个三角函数式,再根据三角函数性质求其值域;(2)可利用降幂公式,倍角公式,差角公式,化为一个角的一个三角函数其值域;(3)利用配方法,并结合二次函数、正弦函数的性质求解;(4)从反函数观点出发,借助于余弦函数的有界性求解.
解:(1)![]() .
.
∵![]() ,∴
,∴![]() .
.
将其利用降幂公式化为一个角的一个三角函数形式,然后利用三角函数的性质求值域.
(2)![]()
![]()
![]()
∵![]() ,
,
∴![]() .
.
利用了降幂公式和倍角公式,将其化为一个角的一个三角函数的形式.
(3)![]() .
.
将其看做关于![]() 的二次函数,注意到
的二次函数,注意到![]() ,
,
∴当![]() 时,
时,![]() .
.
当![]() 时,
时, ![]() ,
,
∴![]() .
.
本题结合了二次函数求极值,但应注意![]() 的取值范围.
的取值范围.
(4)由原式得![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() 或
或![]() .
.
值域为![]() .
.
小结: 配方法、化一法、逆求法、有界性法等,是求三角函数值域常用的几种方法.相信你会从此题的求解过程中,领悟到这一点.
例4.求函数![]() 的单调减区间.
的单调减区间.
分析:容易想到将函数转化为![]() ,换元令
,换元令![]() ,进而转化为
,进而转化为![]() .
.
解:![]() .
.
令![]() ,则
,则![]() .
.
由正弦函数的单调性,知
当![]() (
(![]() )时,函数递减,
)时,函数递减,
即 ![]() (
(![]() ),
),
∴![]() (
(![]() ).
).
∴函数的单调减区间是![]() (
(![]() ).
).
小结:本题通过换元,将函数![]() 化为
化为![]() ,充分体现了转化的数学思想.
,充分体现了转化的数学思想.
例5.作函数![]() 的图像。
的图像。
分析:首先将函数的解析式变形,化为最简形式,然后作函数的图像。
解:当![]() ,即
,即![]() 时,有
时,有![]() ,即
,即![]() 。其图像如图,
。其图像如图,
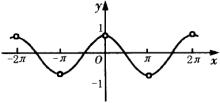
小结:函数![]() 的图像即是
的图像即是![]() 的图像,因此作出
的图像,因此作出![]() 的图像后,要把
的图像后,要把![]() 的这些点去掉。
的这些点去掉。
例6.已知![]() ,(a、b为常数),且
,(a、b为常数),且![]() ,求
,求![]() 。
。
分析:要求函数值,需知函数解析式,因含a、b两个参数,一个条件![]() 难确定。深入分析
难确定。深入分析![]() 与
与![]() 的内在联系,应向函数奇偶性联想。注意到
的内在联系,应向函数奇偶性联想。注意到![]() 为奇函数,问题自可获解。
为奇函数,问题自可获解。
解:因为![]()
![]()
![]() ,所以
,所以![]() 为奇函数,所以
为奇函数,所以![]() ,
,
所以![]() 。
。
小结:(1)判断函数奇偶性时应注意“定义域关于原点对称是函数为奇函数或偶函数的必要条件”的应用。
(2)函数奇偶性的确定,可使研究问题的条件增加,从而使问题难度变小,尤其是自变量互为相反数时的函数值关系问题,可考虑奇偶性的应用。